如图，在四棱锥P-ABCD 中，底面 ABCD 是正方形，侧棱PD底面ABCD，PD=DC=1，点E是PC的中点，作EF
PB交PB于点F.
（Ⅰ）求证：PA∥平面EBD
（Ⅱ）求证：PB平面EFD
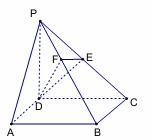
如图，在四棱锥P-ABCD 中，底面 ABCD 是正方形，侧棱PD底面ABCD，PD=DC=1，点E是PC的中点，作EFPB交PB于点F.
（Ⅰ）求证：PA∥平面EBD
（Ⅱ）求证：PB平面EFD
解：连接BE，BD，AC，设AC交BD于G，
则G为AC的中点
在
中，E为PC的中点，
则PA∥EG，
面BED，
面BED (条件少写一个扣2分)
所以
∥平面
..................................... 7分
（2）
PD⊥面ABCD
PD⊥BC
BC⊥CD
（此条件不写扣2分）
PD,CD
面PCD
BC⊥面PCD
面PCD
BC⊥DE
PD=CD，E为PC中点， DE ⊥PC
DE⊥面PBC DE⊥PB，又因为PB⊥EF
平面
......................................1 4分