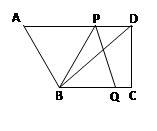（本题满分11分）如图，在直角梯形ABCD中，AD∥BC，∠C＝90°，BC＝16，DC＝12，AD＝21。动点P从点D出发，沿射线DA的方向以每秒2两个单位长的速度运动，动点Q从点C出发，在线段CB上以每秒1个单位长的速度向点B运动，点P，Q分别从点D，C同时出发，当点Q运动到点B时，点P随之停止运动。设运动的时间为t（秒）．
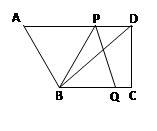
1.（1）设△BPQ的面积为S，求S与t之间的函数关系式
2.（2）当线段PQ与线段AB相交于点O，且2AO＝OB时，求t的值．
3.（3）当t为何值时，以B，P，Q三点为顶点的三角形是等腰三角形？
4.（4）是否存在时刻t，使得PQ⊥BD？若存在，求出t的值；若不存在，请说明理由．
1.（1）s=×12×(16-t)=96-6t…………1分
2.（2）由题意得 △AOP∽△BOQ ∴== ∴BQ=2AP
∴16-t=2(2t-21) ∴t=………2分
3.(3)①若BQ=PQ 则 t2+122=(16-t)2 得t=…………2分
②若BP=BQ 则（16-2t）2+122=(16-t)2 得3t2-32t+144=0 ∵△=322-4×3×144＜0
∴3t2-32t+144=0无解 ∴BP≠BQ…………………2分
③若BP=PQ 则 （16-2t）2+122= t2+122 ∴t=或t=16(不合题意舍去)……………2分
|
|
|
|
 |
4.(4)存在时刻t，使得PQ^BD
过Q作QE^AD，垂足为E，由PQ^BD可知△PQE∽△DBC ∴=
∴ = ∴t=9………………………2分
所以，当t=9时，PQ^BD。
解析:略