在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() 的离心率为
的离心率为![]() ,且过点
,且过点![]() .
.
(1)求![]() 的方程;
的方程;
(2)若动点![]() 在直线
在直线![]() 上,过
上,过![]() 作直线交椭圆
作直线交椭圆![]() 于
于![]() 两点,使得
两点,使得![]() ,再过
,再过![]() 作直线
作直线![]() ,证明:直线
,证明:直线![]() 恒过定点,并求出该定点的坐标.
恒过定点,并求出该定点的坐标.
在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() 的离心率为
的离心率为![]() ,且过点
,且过点![]() .
.
(1)求![]() 的方程;
的方程;
(2)若动点![]() 在直线
在直线![]() 上,过
上,过![]() 作直线交椭圆
作直线交椭圆![]() 于
于![]() 两点,使得
两点,使得![]() ,再过
,再过![]() 作直线
作直线![]() ,证明:直线
,证明:直线![]() 恒过定点,并求出该定点的坐标.
恒过定点,并求出该定点的坐标.
(1)由题意知![]() ,
,
又椭圆的离心率为![]() ,所以
,所以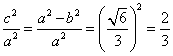 ,
,
所以![]() ,
,
所以椭圆![]() 的方程为
的方程为![]() .
.
(2)因为直线![]() 的方程为
的方程为![]() ,设
,设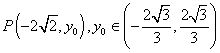 ,
,
①当![]() 时,设
时,设![]() ,显然
,显然![]() ,
,
由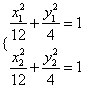 可得
可得![]() ,即
,即![]() ,
,
又![]() ,所以
,所以![]() 为线段
为线段![]() 的中点,
的中点,
故直线![]() 的斜率为
的斜率为![]() ,
,
又![]() ,
,
所以直线![]() 的方程为
的方程为![]()
即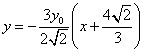 ,显然
,显然![]() 恒过定点
恒过定点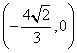 ,
,
②当![]() 时,
时, ![]() 过点
过点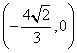 ,
,
综上可得直线![]() 过定点
过定点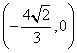 .
.