如图甲，分别以两个彼此相邻的正方形OABC与CDEF的边OC、OA所在直线为

如图甲，分别以两个彼此相邻的正方形OABC与CDEF的边OC、OA所在直线为x轴、y轴建立平面直角坐标系（O、C、F三点在x轴正半轴上）.若⊙P过A、B、E三点(圆心在x轴上)，抛物线经过A、C两点，与x轴的另一交点为G，M是FG的中点，正方形CDEF的面积为1.
（1）求B点坐标；
（2）求证：ME是⊙P的切线；
（3）设直线AC与抛物线对称轴交于N，Q点是此对称轴上不与N点重合的一动点，①求△ACQ周长的最小值；②若FQ＝t，S_△ACQ＝S，直接写出S与t之间的函数关系式.

解：（1）如图甲，连接PE、PB，设PC＝n
∵正方形CDEF面积为1∴CD＝CF＝1
根据圆和正方形的对称性知OP＝PC＝n
∴BC＝2PC＝2n
而PB＝PE，

∴
解得n=1   (舍去)
∴BC＝OC＝2  ∴B点坐标为（2，2）

（2）如图甲，由（1）知A（0，2），C（2，0）
∵A，C在抛物线上∴     ∴

∴抛物线的解析式为

即
∴抛物线的对称轴为x=3,即EF所在直线
∵C与G关于直线x=3对称， ∴CF＝FG＝1  ∴FM＝FG＝
在Rt△PEF与Rt△EMF中
＝，  ∴=∴△PEF∽△EMF
∴∠EPF＝∠FEM∴∠PEM＝∠PEF+∠FEM＝∠PEF+∠EPF＝90°
∴ME与⊙P相切
（注：其他方法，参照给分）

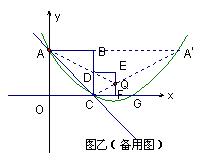
（3）①如图乙，延长AB交抛物线于，连交对称轴x=3于Q，连AQ则有AQ＝Q，△ACQ周长的最小值为（AC+C）的长
∵A与关于直线x=3对称∴A（0，2），（6，2）
∴C＝（6-2），

而AC=

∴△ACQ周长的最小值为

③    当Q点在F点上方时，S＝t+1

④    当Q点在线段FN上时，S＝1-t

⑤    当Q点在N点下方时，S＝t-1