如图所示，直线y1=与x轴交于点A，与y轴交于点C，与反比例函数y2=（x

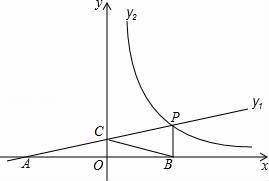
如图所示，直线y₁=与x轴交于点A，与y轴交于点C，与反比例函数y₂=（x＞0）的图象交于点P，作PB⊥x轴于点B，且AC=BC．

（1）求点P的坐标和反比例函数y₂的解析式；

（2）请直接写出y₁＞y₂时，x的取值范围；

（3）反比例函数y₂图象上是否存在点D，使四边形BCPD为菱形？如果存在，求出点D的坐标；如果不存在，说明理由．

【分析】（1）首先求得直线与x轴和y轴的交点，根据AC=BC可得OA=OB，则B的坐标即可求得，BP=2OC，则P的坐标可求出，然后利用待定系数法即可求得函数的解析式；

（2）求y₁＞y₂时x的取值范围，就是求直线位于反比例函数图象上边时对应的x的范围；

（3）连接DC与PB交于点E，若四边形BCPD是菱形时，CE=DE，则CD的长即可求得，从而求得D的坐标，判断D是否在反比例函数的图象上即可．

【解答】解：（1）∵一次函数y₁=x+1的图象与x轴交于点A，与y轴交于点C，

∴A（﹣4，0），C（0，1），

又∵AC=BC，CO⊥AB，

∴O是AB的中点，即OA=OB=4，且BP=2OC=2，

∴P的坐标是（4，2），

将P（4，2）代入y₂=得m=8，即反比例函数的解析式为y₂=；

（2）当x＞4时，y₁＞y₂；

（3）假设存在这样的点D，使四边形BCPD为菱形，如图所示，连接DC与PB交于点E．

∵四边形BCPD是菱形，

∴CE=DE=4，

∴CD=8，

将x=8代入反比例函数解析式y=得y=1，

∴D的坐标是（8，1），即反比例函数的图象上存在点D使四边形BCPD是菱形，此时D的坐标是（8，1）．

【点评】本题考查了一次函数、反比函数以及菱形的判定与性质的综合应用，理解菱形的性质求得D的坐标是关键．