a.
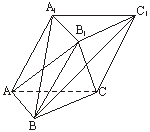
20题图
(Ⅰ)求异面直线AC与BC1所成角的余弦值；
(Ⅱ)求证A1B⊥面AB1C.
a.
20题图
(Ⅰ)求异面直线AC与BC1所成角的余弦值；
(Ⅱ)求证A1B⊥面AB1C.
解:过点B作BO⊥AC,垂足为点O,则BO⊥侧面ACC1A1,连结A1O,
在Rt△A1BO中,A1B＝
a,∴A1O＝
.∴△A1AO为直角三角形,A1O⊥AC,A1O⊥底面ABC.
解法一:
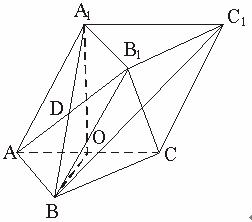
(Ⅰ)
∵ A1C1∥AC,
∴ ∠BC1A1为异面直线AC与BC1所成的角.
∵ A1O⊥面ABC,AC⊥BO,
∴ AC⊥A1B,
∴ A1C1⊥A1B.
在Rt△A1BC1中,A1B＝
∴ BC1＝
∴cosBC
所以,异面直线AC与BC1所成角的余弦值为
(Ⅱ)
设A1B与AB1相交于点D,
∵ ABB1A1为菱形,
∴ AB1⊥A1B.
又 A1B⊥AC,
AB1与AC是平面AB1C内两条相交直线,
所以A1B⊥面AB1C.
解法二:
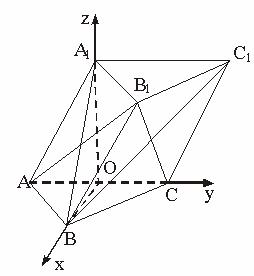
(Ⅰ)如图,建立坐标系,原点为BO⊥AC的垂足O.由题设条件可得
B(
a),A(0,－
a,0),∴ 
a,a,
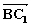
a),＝(0,a,0).
设
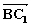的夹角为θ,则cosθ＝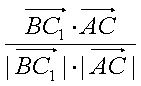
＝
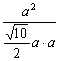,所以,异面直线AC与BC1所成角的余弦值为
(Ⅱ)A1(0,0,
,0,0),∴ 
a,0,－
a), 
·
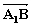
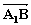＝0.∴ A1B⊥AC1.
又ABB1A1为菱形,
∴ A1B⊥AB1.
又因为AB1与AC为平面AB1C内两条相交直线,
所以A1B⊥平面AB1C.