如图,在△ABC中,AB=AC,∠ABC、∠ACB的平分线BD,CE相交于O点,且BD交AC于点D,CE交AB于点E,某同学分析图形后得出以下结论,上述结论一定正确的是 (填代号).
①△BCD≌△CBE;②△BAD≌△BCD;③△BDA≌△CEA;④△BOE≌△COD;⑤△ACE≌△BCE.


如图,在△ABC中,AB=AC,∠ABC、∠ACB的平分线BD,CE相交于O点,且BD交AC于点D,CE交AB于点E,某同学分析图形后得出以下结论,上述结论一定正确的是 (填代号).
①△BCD≌△CBE;②△BAD≌△BCD;③△BDA≌△CEA;④△BOE≌△COD;⑤△ACE≌△BCE.


①③④ (填代号).
①△BCD≌△CBE;②△BAD≌△BCD;③△BDA≌△CEA;④△BOE≌△COD;⑤△ACE≌△BCE.
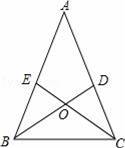

【考点】全等三角形的判定.
【分析】由AB=AC,∠ABC、∠ACB的平分线BD,CE相交于O点,得出各相等的边角,再依据全等三角形的判定定理即可判定五个答案哪个一定成立.
【解答】解:∵AB=AC,
∴∠EBC=∠DCB,
又∵BD平分∠ABC,∠CE平分∠ACB,
∴∠DBC=∠ECB,
∵∠BEC=180°﹣∠EBC﹣∠ECB,∠CDB=180°﹣∠DCB﹣∠DBC,
∴∠BEC=∠CDB.
在△EBC和△DCB中,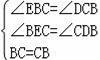
 ,
,
∴△EBC≌△DCB(AAS).
即①成立;
在△BAD和△BCD中,仅有![]()
![]() ,
,
不满足全等的条件,
即②不一定成立;
∵△EBC≌△DCB,
∴BD=CE.
在△BDA和△CEA中,
 ,
,
∴△BDA≌△CEA(SAS).
即③成立;
∵△BDA≌△CEA,
∴AD=AE,
∵AB=AC,
∴BE=CD.
在△BOE和△COD中,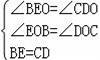
 ,
,
∴△BOE≌△COD(AAS).
即④成立;
在△ACE和△BCE中,仅有![]()
![]() ,
,
不满足全等的条件,
即⑤不一定成立.
综上可知:一定成立的有①③④.
故答案为:①③④.

