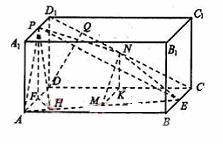
(Ⅰ)求证:![]()
(Ⅱ)求二面角![]()
(Ⅲ)求三棱锥![]()

(Ⅰ)求证:![]()
(Ⅱ)求二面角![]()
(Ⅲ)求三棱锥![]()
本小题主要考察长方体的概念、直线和平面、平面和平面的关系等基础知识,以及空间想象能力和推理能力。
解法一:(Ⅰ)证明:取![]()
∵![]()
∵![]()
∴![]()
∴面![]()

(Ⅱ)设![]()
∵![]()
作![]()
从而![]()
在![]()
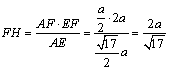
在![]()
故:二面角![]()
(Ⅲ)![]()
作![]()
∴![]()
∴在![]()
∴![]()
解法二:以![]()
![]()
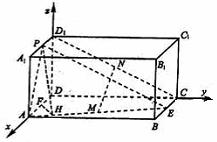
∵![]()
∴![]()
(Ⅰ)![]()
取n
=(0,1,0),显然n ![]()
又![]()
(Ⅱ)过![]()
设![]()
又![]()
由![]()
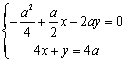
解得![]()
∴![]()
∴![]()
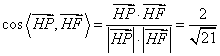
故:二面角![]()
(Ⅲ)设n1
=(x1,y1,z1)为平面 又![]()
∴ 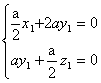
即 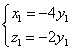
∴可取n1
=(4,-1,2) ∴![]()
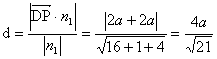
∵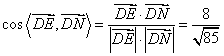
∴![]()
∴![]()