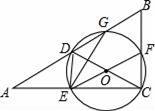
如图，在△ABC中，∠ACB=90°，D是AB的中点，以DC为直径的⊙O交△ABC的

如图，在△ABC中，∠ACB=90°，D是AB的中点，以DC为直径的⊙O交△ABC的边于G，F，E点．

（1）求证：F为BC边的中点；

（2）判断四边形BDEF的形状，并说明你的理由；

（3）若∠A=35°，求弧的度数．

【考点】圆的综合题．

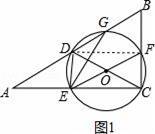
【分析】（1）连接DF，如图1，根据直角三角形斜边上的中线性质得到BD=AD=CD，再利用圆周角定理得到∠DFC=90°，然后根据等腰三角形的性质可得BF=FC；

（2）与（1）一样可得E为AC中点，则利用三角形中位线性质得DE=BC，DE∥BC，所以DE=CF，DE∥CF，于是可判断四边形BDEF是平行四边形；

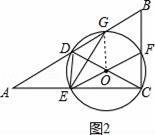
（2）连接OG，如图2，先利用等腰三角形的性质由CD=AD得到∠DCA═∠A=35°，则利用三角形外角性质得∠ODG=70°，再根据等腰三角形的性质和三角形内角和定理得∠DOG=40°，然后根据圆心角的度数等于它所对弧的度数得到的度数．

【解答】（1）证明：连接DF，如图1，

∵∠ACB=90°，D是AB的中点，

∴BD=AD=CD，

∵CD是⊙O的直径，

∴∠DFC=90°，

∴BF=FC，

即F是BC的中点；

（2）解：四边形BDEF为平行四边形．理由如下：

与（1）一样可得E为AC中点，

∴DE是△ABC的中位线，

∴DE=BC，DE∥BC，

而BF=CF，

∴DE=CF，DE∥CF，

∴四边形BDEF是平行四边形；

（2）解：连接OG，如图2，

∵CD=AD，

∴∠DCA═∠A=35°，

∴∠ODG=∠A+∠DCA=70°，

∵OD=OG，

∴∠OGD=∠ODG=70°，

∴∠DOG=180°﹣2×70°=40°，

即的度数为40°．

【点评】本题考查了圆的综合题：熟练掌握圆周角定理、等腰直角三角形的性质、直角三角形斜边上的中线性质和平行四边形的判定方法．充分利用三角形中位线的性质．