首页 / 8个人排成一排，其中甲、乙、丙3人中，有两个相邻，但这3个人不同

8个人排成一排，其中甲、乙、丙3人中，有两个相邻，但这3个人不同

8个人排成一排，其中甲、乙、丙3人中，有两个相邻，但这3个人不同时相邻，求满足条件的所有不同排法的种数.

答案

分析：通过审题发现，这是一道典型的排列问题，对于排列中元素必须在一起时，常把它们看作一个整体，然后考虑其内部的位置关系；对于排列中不能相邻的元素，采用插空的方式来处理.

解法一：（直接插入法）先排甲、乙、丙以外的5个人，有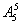

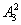
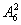
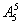
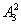
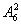
种排法；再从甲、乙、丙3个人中选2人合并为一个元素，和余下的1个人插入6个空中，有·种插排法，故总的排法为··=21 600种.

解法二：（间接法）先将8个人进行全排列，有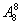

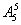
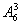
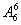
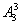
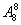
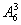
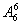
种排法，其中:①甲、乙、丙3个人两两都不相邻的排法有种；②甲、乙、丙3个人同时相邻的排法有种.故共有排法-（+）=21 600种.

相关题目

糖类、油脂、蛋白质是维持人体生命活动所必需的三大营养
糖类、油脂、蛋白质是维持人体生命活动所必需的三大营养物质，下列叙述正确的是（ ） A.植物油不能使溴的四氯化碳溶液褪色B.淀粉水解的最终
被切除某一内分泌器官的褐家鼠会很快死亡，若补充大量食
被切除某一内分泌器官的褐家鼠会很快死亡，若补充大量食盐水可维持生存。切除的这一内分泌器官最可能是 A.甲状腺                     B.
读“我国能源区域分布和能源调运线路图”，分析回答下列
读“我国能源区域分布和能源调运线路图”，分析回答下列问题： (1) 图中A、B代表我国正在建设的两大能源工程，它们分别是“             
大型油轮如果通不过苏伊士运河，必须绕道从波斯湾到欧洲
大型油轮如果通不过苏伊士运河，必须绕道从波斯湾到欧洲，则必经之地为（  ） A.直布罗陀海峡                         B.好望角 C.马六甲
人生在平淡中寻找幸福，在细微中品味幸福，在孤独中守望
人生在平淡中寻找幸福，在细微中品味幸福，在孤独中守望幸福，在遗忘中怀念幸福。幸福的生活需要哲学的指引，这是因为（    ） A.哲学是使人聪
I         along the street looking for a place to park when the accident
I         along the street looking for a place to park when the accident         .        A．went; was occurring B．went; occurred        C．was going; occurred D．was
I used to hate myself because I wasn’t “normal”. Everyone else could play
I used to hate myself because I wasn’t “normal”. Everyone else could play on the monkey bars and ride on a bicycle, but not   16  . I had a severe spinal cord disorder (脊髓病) and I knew
 阅读下面的材料，按要求回答问题。（4分） 亲爱的孩子，
 阅读下面的材料，按要求回答问题。（4分） 亲爱的孩子，你走后第二天，就想写信，怕你嫌烦，也就罢了。可是没一天不想着你，每天清早六七点就

最新题目

分别选出下列各题中对文言句子的翻译有误的一项。 A．木直
传染病的传播共有三个基本环节，其中属于传染源的是（ 
如图，直线a∥b，点B在a上，且AB⊥BC．若∠1=35°，那么∠2等
已知乙苯的结构简式为C6H5—C2H5，其一氯代物的同分异构体有
陆机《文赋》指出，写作的奥秘之一是“立片言而居要，乃
读下表，完成下列问题。 国家人口出生率（%）人口死亡率（
选出下列句子中没有错别字的一项。 A.      我想，他要说
三根平行的长直导线分别垂直地通过一个等腰直角三角形的
.下列各条款不属于《辛丑条约》的是(   ) A.严禁人民参加反
选出加点词活用情况相同的一项（      ） A、风乎舞雩  
某电子体重计的电路如图所示，其中弹簧上端和滑动变阻器
国庆前夕，某中学举行了一次以 “回顾中国近现代化的里程
对下列两幅图片的理解最为准确的是（   ） A．春秋争霸 
“大将筹边尚未还，湖湘子弟满天山；新栽杨柳三千里，引
下表是抗战时期，中日双方报刊上登载的部分战役中日方伤
在包含太阳和地球的天体系统中，最高一级和最低一级的天
下列叙述正确的是（    ） A. 纯碱、烧碱均属碱 B. 、均属
下列对加点词解释有误的一项是（   ） A.既克，公问其故 
联合国与国际联盟的区别是    A．都是世界大战的产物   
如图13-1所示，物体A从高h的P处沿光滑曲面从静止开始下滑，