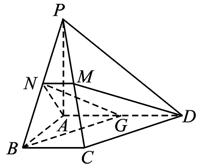
(Ⅰ)求证：PB⊥DM；
(Ⅱ)求CD与平面ADMN所成的角.
(Ⅰ)求证：PB⊥DM；
(Ⅱ)求CD与平面ADMN所成的角.
方法一：
(Ⅰ)因为N是PB的中点，PA=AB，所以AN⊥PB.
因为AD⊥平面PAB，所以AD⊥PB，从而PB⊥平面ADMN.
因为DM
平面ADMN，所以PB⊥DM.
(Ⅱ)取AD的中点G，连结BG、NG，则BG∥CD，
所以BG与平面ADMN所成的角和CD与平面ADMN所成的角相等.
因为PB⊥平面ADMN，所以∠BGN是BG与平面ADMN所成的角.
在Rt△BGN中，sin∠BGN=
.
故CD与平面ADMN所成的角是arcsin
.
方法二：如图，以A为坐标原点建立空间直角坐标系A-xyz,设BC=1，则A(0，0，0)，P(0，0，2)，B(2，0，0)，C(2，1，0)，M(1，
，1)，D(0，2，0).
(Ⅰ)因为
·
=(2，0，-2)·(1，-
，1)=0，
所以PB⊥DM.
(Ⅱ)因为
·
=(2，0，-2)·(0，2，0)=0，
所以PB⊥AD，
又因为PB⊥DM，
所以PB⊥平面ADMN.
因此〈
，
〉的余角即是CD与平面ADMN所成的角.
因为cos〈
,
〉=
=
，
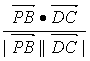所以CD与平面ADMN所成的角为arcsin
.