如图15所示,△ABC和△BCD所在平面互相垂直,且AB=BC=BD=2,∠ABC=∠DBC=120°,E,F分别为AC,DC的中点.
(1)求证:EF⊥BC;
(2)求二面角EBFC的正弦值.
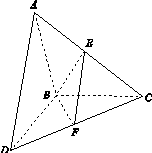
图15
如图15所示,△ABC和△BCD所在平面互相垂直,且AB=BC=BD=2,∠ABC=∠DBC=120°,E,F分别为AC,DC的中点.
(1)求证:EF⊥BC;
(2)求二面角EBFC的正弦值.

图15
.解:(1)证明:方法一,过点E作EO⊥BC,垂足为O,连接OF.由△ABC≌△DBC可证出△EOC≌△FOC,所以∠EOC=∠FOC=![]() ,即FO⊥BC.又EO⊥BC,EO∩FO=O,所以BC⊥平面EFO.又EF⊂平面EFO,所以EF⊥BC.
,即FO⊥BC.又EO⊥BC,EO∩FO=O,所以BC⊥平面EFO.又EF⊂平面EFO,所以EF⊥BC.

图1
方法二,由题意,以B为坐标原点,在平面DBC内过B作垂直BC的直线,并将其作为x轴,BC所在直线为y轴,在平面ABC内过B作垂直BC的直线,并将其作为z轴,建立如图所示的空间直角坐标系,易得B(0,0,0),A(0,-1,![]() ),D(
),D(![]() ,-1,0),C(0,2,0),因而E(0,
,-1,0),C(0,2,0),因而E(0,![]() ,
,![]() ),F(
),F(![]() ,
,![]() ,0),所以
,0),所以![]() =(
=(![]() ,0,-
,0,-![]() ),
),![]() =(0,2,0),因此
=(0,2,0),因此![]() ·
·![]() =0,
=0,
从而![]() ⊥
⊥![]() ,所以EF⊥BC.
,所以EF⊥BC.
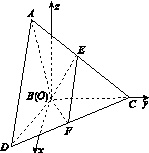
图2
(2)方法一,在图1中,过点O作OG⊥BF,垂足为G,连接EG.因为平面ABC⊥平面BDC,所以EO⊥面BDC,又OG⊥BF,所以由三垂线定理知EG⊥BF,
因此∠EGO为二面角EBFC的平面角.
在△EOC中,EO=![]() EC=
EC=![]() BC·cos 30°=
BC·cos 30°=![]() .
.
由△BGO∽△BFC知,OG=![]() ·FC=
·FC=![]() ,因此tan∠EGO=
,因此tan∠EGO=![]() =2,从而得sin∠EGO=
=2,从而得sin∠EGO=![]() ,即二面角EBFC的正弦值为
,即二面角EBFC的正弦值为![]() .
.
方法二,在图2中,平面BFC的一个法向量为n1=(0,0,1).
设平面BEF的法向量n2=(x,y,z),
又![]() =(
=(![]() ,
,![]() ,0),
,0),![]() =(0,
=(0,![]() ,
,![]() ),
),
所以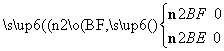 得其中一个n2=(1,-
得其中一个n2=(1,-![]() ,1).
,1).
设二面角EBFC的大小为θ,且由题知θ为锐角,则cos θ=|cos〈n1,n2〉|=![]() =
=![]() ,
,
因此sin θ=![]() =
=![]() ,即所求二面角正弦值为
,即所求二面角正弦值为![]() .
.