еҰӮеӣҫпјҲеҚҒдә”пјүпјҢжҠӣзү©зәҝ пјҲе…¶дёӯ
пјҲе…¶дёӯ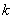 дёәжӯЈж•ҙж•°пјүдёҺxиҪҙзӣёдәӨдәҺдёӨдёӘВ
дёәжӯЈж•ҙж•°пјүдёҺxиҪҙзӣёдәӨдәҺдёӨдёӘВ
В В В дёҚеҗҢзҡ„зӮ№AгҖҒBпјҲзӮ№AдҪҚдәҺзӮ№Bзҡ„е·Ұдҫ§пјүпјҢдёҺyиҪҙзӣёдәӨдәҺзӮ№CпјҢиҝһз»“ACгҖҒBCпјҺ
пјҲ1пјүжұӮ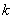 зҡ„еҖјпјӣпјҲ2еҲҶпјү
зҡ„еҖјпјӣпјҲ2еҲҶпјү
пјҲ2пјүеҰӮеӣҫв‘ пјҢи®ҫзӮ№DжҳҜзәҝж®өACдёҠзҡ„дёҖеҠЁзӮ№пјҢдҪңDEвҠҘxиҪҙдәҺзӮ№FпјҢдәӨжҠӣзү©зәҝдәҺзӮ№EпјҢжұӮ
зәҝж®өDEй•ҝеәҰзҡ„жңҖеӨ§еҖјпјӣпјҲ4еҲҶпјү
пјҲ3пјүеҰӮеӣҫв‘ЎпјҢжҠӣзү©зәҝдёҠжҳҜеҗҰеӯҳеңЁзӮ№MпјҢиҝҮзӮ№MдҪңMNеһӮзӣҙxиҪҙдәҺзӮ№NпјҢдҪҝеҫ—д»ҘзӮ№AгҖҒMгҖҒNдёәйЎ¶зӮ№зҡ„дёүи§’еҪўдёҺв–іABCзӣёдјјпјҹиӢҘеӯҳеңЁпјҢжұӮеҮәзӮ№Mзҡ„еқҗж ҮпјӣиӢҘдёҚеӯҳеңЁпјҢиҜ·иҜҙжҳҺзҗҶз”ұпјҺпјҲ4еҲҶпјү

В В В
В и§ЈпјҲ1пјүз”ұ йўҳж„Ҹеҫ—
йўҳж„Ҹеҫ— пјһ0пјҢи§Јеҫ—
пјһ0пјҢи§Јеҫ—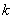 пјң
пјң
вҲө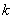 дёәжӯЈж•ҙж•°пјҢвҲҙ
дёәжӯЈж•ҙж•°пјҢвҲҙ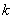 =1.В В В В В В В В В В В В В В В В вҖҰвҖҰ2еҲҶ
=1.В В В В В В В В В В В В В В В В вҖҰвҖҰ2еҲҶ
пјҲ2пјүз”ұ пјҢеҫ—
пјҢеҫ— пјҢ
пјҢ .вҲҙзӮ№AпјҲпјҚ4пјҢ0пјүпјҢBпјҲ1пјҢ0пјү.
.вҲҙзӮ№AпјҲпјҚ4пјҢ0пјүпјҢBпјҲ1пјҢ0пјү.
д»Ө пјҢеҫ—
пјҢеҫ— пјҢвҲҙзӮ№Cзҡ„еқҗж ҮдёәпјҲ0пјҢ2пјү. вҖҰвҖҰ3еҲҶ
пјҢвҲҙзӮ№Cзҡ„еқҗж ҮдёәпјҲ0пјҢ2пјү. вҖҰвҖҰ3еҲҶ
и®ҫзӣҙзәҝACзҡ„и§ЈжһҗејҸдёә пјҢеҲҷ
пјҢеҲҷ пјҢвҲҙ
пјҢвҲҙ
В вҲҙ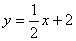 . В вҖҰвҖҰ4еҲҶ
. В вҖҰвҖҰ4еҲҶ
В В В В и®ҫEпјҲmпјҢ )пјҢвҲҙD(mпјҢ
)пјҢвҲҙD(mпјҢ m+2)
m+2)
В В В вҲҙDE= пјҚ(
пјҚ( m+2) =
m+2) = m2пјҚ2m=
m2пјҚ2m=

еҪ“m=пјҚ2ж—¶пјҢDEзҡ„жңҖеӨ§еҖјжҳҜ2 вҖҰвҖҰ6еҲҶ
пјҲ3пјүеңЁRtО”AOCдёӯпјҢ ,еңЁRtО”BOCдёӯпјҢ
,еңЁRtО”BOCдёӯпјҢ
В В В вҲө пјҢвҲҙвҲ ACB=900. еҸҲCOвҠҘABпјҢ
пјҢвҲҙвҲ ACB=900. еҸҲCOвҠҘABпјҢ
В В В вҲҙ О”ABCвҲҪО”ACOвҲҪО”CBO.В В вҖҰвҖҰ7еҲҶ
В в‘ иӢҘзӮ№MеңЁ иҪҙдёҠж–№ж—¶пјҢеҪ“MзӮ№дёҺCзӮ№йҮҚеҗҲпјҢеҚіMпјҲ0пјҢ2пјүж—¶пјҢО”MANвҲҪО”BACпјӣ
иҪҙдёҠж–№ж—¶пјҢеҪ“MзӮ№дёҺCзӮ№йҮҚеҗҲпјҢеҚіMпјҲ0пјҢ2пјүж—¶пјҢО”MANвҲҪО”BACпјӣ
ж №жҚ®жҠӣзү©зәҝзҡ„еҜ№з§°жҖ§пјҢеҪ“M(пјҚ3,2) ж—¶пјҢО”MANвҲҪО”ABCпјӣвҖҰвҖҰ8еҲҶ
В в‘ЎиӢҘзӮ№MеңЁ иҪҙдёӢж–№ж—¶пјҢи®ҫN(n,0)пјҢеҲҷMпјҲn,
иҪҙдёӢж–№ж—¶пјҢи®ҫN(n,0)пјҢеҲҷMпјҲn,  пјүпјҢ
пјүпјҢ
В В В В В В вҲҙ MN= n2+
n2+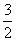 nпјҚ2 ,В AN=n+4
nпјҚ2 ,В AN=n+4
В В В В В В еҪ“ ж—¶пјҢMN=
ж—¶пјҢMN= ANпјҢ
ANпјҢ
В еҚі n2+
n2+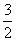 nпјҚ2=
nпјҚ2= (n+4)пјҢ
(n+4)пјҢ
В В В В В В n2+2nпјҚ8=0 пјҢвҲҙ n1= пјҚ4(иҲҚеҺ»), n2=2пјҢ
вҲҙMпјҲ2пјҢпјҚ3пјүВ В В В вҖҰвҖҰ9еҲҶ
В В В В В В еҪ“ ж—¶пјҢMN=2ANпјҢ
ж—¶пјҢMN=2ANпјҢ
еҚі n2+
n2+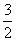 nпјҚ2=2(n+4)пјҢ
nпјҚ2=2(n+4)пјҢ
n2пјҚnпјҚ20=0 пјҢвҲҙ n1= пјҚ4(иҲҚеҺ»)пјҢn2=5пјҢ
вҲҙMпјҲ5пјҢпјҚ18пјү
В В В В В В з»јдёҠжүҖиҝ°пјҡеӯҳеңЁM1пјҲ0пјҢ2пјү,M2(пјҚ3,2),
 M3пјҲ2пјҢпјҚ3пјү,M4пјҲ5пјҢпјҚ18пјү, дҪҝеҫ—д»ҘзӮ№
M3пјҲ2пјҢпјҚ3пјү,M4пјҲ5пјҢпјҚ18пјү, дҪҝеҫ—д»ҘзӮ№
В В В В В В В AгҖҒMгҖҒNдёәйЎ¶зӮ№зҡ„дёүи§’еҪўдёҺв–іABCзӣёдјј..В
![]() пјҲе…¶дёӯ
пјҲе…¶дёӯ![]() дёәжӯЈж•ҙж•°пјүдёҺxиҪҙзӣёдәӨдәҺдёӨдёӘВ
дёәжӯЈж•ҙж•°пјүдёҺxиҪҙзӣёдәӨдәҺдёӨдёӘВ ![]() зҡ„еҖјпјӣпјҲ2еҲҶпјү
зҡ„еҖјпјӣпјҲ2еҲҶпјү

