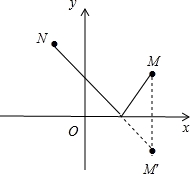
已知两点M（3，2），N（﹣1，3），点P是x轴上一动点，若使PM+PN最短，则点P的坐标应为( )
A．（0，
） B．（
，0） C．（
，0） D．（
，0）
已知两点M（3，2），N（﹣1，3），点P是x轴上一动点，若使PM+PN最短，则点P的坐标应为( )
A．（0，） B．（，0） C．（，0） D．（，0）
D【考点】轴对称-最短路线问题；坐标与图形性质．
【分析】先求得M的对称点M′的坐标，根据两点的坐标代入一次函数解析式中，确定一次函数解析式，然后根据点P在x轴上，则其纵坐标是0，求出横坐标即可．
【解答】解：作M点关于x轴的对称点M′，
∵M（3，2），
∴M′（3，﹣2），
设直线M′N的解析式为y=kx+b，
∴
，
解得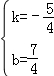
，
∴直线M′N的解析式为y=﹣
x+
，
∵P的纵坐标为0，
∴﹣x+=0，解得x=
，
∴P（，0）．
故选D．
【点评】此题考查了最短路径问题和用待定系数法求一次函数解析式，判断出M、P、N三点共线时MN最小是解题的关键．