已知抛物线![]() 的顶点为坐标原点,焦点为
的顶点为坐标原点,焦点为![]() .
.
(Ⅰ)求抛物线![]() 的方程;
的方程;
(Ⅱ)若点![]() 为抛物线
为抛物线![]() 的准线上的任意一点,过点
的准线上的任意一点,过点![]() 作抛物线
作抛物线![]() 的切线
的切线![]() 与
与![]() ,切点
,切点
分别为![]() ,求证:直线
,求证:直线![]() 恒过某一定点;
恒过某一定点;
(Ⅲ)分析(Ⅱ)的条件和结论,反思其解题过程,再对命题(Ⅱ)进行变式和推广.请写出一个你发现的真命题,不要求证明(说明:本小题将根据所给出的命题的正确性和一般性酌情给分).
已知抛物线![]() 的顶点为坐标原点,焦点为
的顶点为坐标原点,焦点为![]() .
.
(Ⅰ)求抛物线![]() 的方程;
的方程;
(Ⅱ)若点![]() 为抛物线
为抛物线![]() 的准线上的任意一点,过点
的准线上的任意一点,过点![]() 作抛物线
作抛物线![]() 的切线
的切线![]() 与
与![]() ,切点
,切点
分别为![]() ,求证:直线
,求证:直线![]() 恒过某一定点;
恒过某一定点;
(Ⅲ)分析(Ⅱ)的条件和结论,反思其解题过程,再对命题(Ⅱ)进行变式和推广.请写出一个你发现的真命题,不要求证明(说明:本小题将根据所给出的命题的正确性和一般性酌情给分).
本题主要考查抛物线的标准方程与性质、直线与抛物线的位置关系、归纳推理等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、数形结合思想、特殊与一般思想等.
解:(Ⅰ)依题意可设抛物线![]() 的方程为:
的方程为:![]() (
(![]() ).
).
由焦点为![]() 可知
可知![]() ,所以
,所以![]() .
.
所以所求的抛物线方程为![]() .····················· 4分
.····················· 4分
(Ⅱ)方法一:
设切点![]() 、
、![]() 坐标分别为
坐标分别为![]() ,由(Ⅰ)知,
,由(Ⅰ)知,![]() .
.
则切线![]() 的斜率分别为
的斜率分别为![]() ,
,
故切线![]() 的方程分别为
的方程分别为![]() ,
,![]() ,··· 5分
,··· 5分
联立以上两个方程,得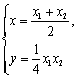 .故
.故![]() 的坐标为
的坐标为![]() ,······· 6分
,······· 6分
因为点![]() 在抛物线
在抛物线![]() 的准线上,所以
的准线上,所以![]() ,即
,即![]() .········ 7分
.········ 7分
设直线![]() 的方程为
的方程为![]() ,代入抛物线方程
,代入抛物线方程![]() ,得
,得![]() ,
,
所以![]() ,即
,即![]() ,所以
,所以![]() .················· 9分
.················· 9分
故![]() 的方程为
的方程为![]() ,故直线
,故直线![]() 恒过定点
恒过定点![]() .············ 10分
.············ 10分
方法二:设切点![]() 、
、![]() 坐标分别为
坐标分别为![]() ,设
,设![]() ,
,
易知直线![]() 斜率必存在,可设过点
斜率必存在,可设过点![]() 的切线方程为
的切线方程为![]() .
.
由![]() ,消去
,消去![]() 并整理得
并整理得![]() .······ ①
.······ ①
因为切线与抛物线有且只有一个交点,
所以![]() ,整理得
,整理得![]() ,········· ②
,········· ②
所以直线![]() 斜率
斜率![]() 为方程②的两个根,故
为方程②的两个根,故![]() ,········· 5分
,········· 5分
另一方面,由![]() 可得方程①的解为
可得方程①的解为![]() ,
,
所以![]() .·························· 6分
.·························· 6分
假设存在一定点,使得直线![]() 恒过该定点,则由抛物线对称性可知该定点必在
恒过该定点,则由抛物线对称性可知该定点必在![]() 轴
轴
上,设该定点为![]() ,························· 7分
,························· 7分
则![]() .所以
.所以![]() ,
,
所以![]() ,整理得
,整理得![]() 所以
所以![]() ,
,
所以![]() ························· 9分
························· 9分
所以直线![]() 过定点
过定点![]() .························ 10分
.························ 10分
(Ⅲ)结论一:若点![]() 为直线
为直线![]() (
(![]() )上的任意一点,过点
)上的任意一点,过点![]() 作抛物线
作抛物线![]()
![]() (
(![]() )的切线
)的切线![]() ,切点分别为
,切点分别为![]() ,则直线
,则直线![]() 恒过定点
恒过定点![]() .················· 14分
.················· 14分
结论二:过点![]() (
(![]() )任作一条直线交抛物线
)任作一条直线交抛物线![]()
![]() 于
于![]() 两点,分别以点
两点,分别以点![]() 为切点作该抛物线的切线,两切线交于点
为切点作该抛物线的切线,两切线交于点![]() ,则点
,则点![]() 必在定直线
必在定直线![]() 上.
上.
···································· 14分
结论三:已知点![]() 为直线
为直线![]() 上的一点,若过点
上的一点,若过点![]() 可以作两条直线与抛物线
可以作两条直线与抛物线![]()
![]() (
(![]() )相切,切点分别为
)相切,切点分别为![]() ,则直线
,则直线![]() 恒过定点
恒过定点![]() .·················· 14分
.·················· 14分
说明:①以上两结论只要给出其中一个即可或给出更一般性的结论;
②以上两结论中的抛物线开口方向均可改变;
③该小题评分可对照以下表格分等级给分:
| 得分 | 答题情况 |
| 0分 | 写出与命题(ⅰ)无关的结论. |
| 所给命题的条件与结论均存在问题. | |
| 1分 | 将准线或抛物线改为其它特殊情况,结论正确. |
| 将准线或抛物线其中一个一般化,但结论中的定点(或定直线)有误. | |
| 2分 | 写出命题的逆命题,结论正确.( 其它分点逆命题相应给分) |
| 将准线和抛物线都推广成一般情况,但结论中的定点(或定直线)有误. | |
| 3分 | 将准线和抛物线其中一个推广成一般情况,结论正确. |
| 将准线和抛物线都推广成一般情况,但 | |
| 4分 | 将准线和抛物线都推广成一般情况,结论正确. |