22.设P1(x1,y1),P2(x2,y2),…,Pn(xn,yn)(n≥3,n∈N)是二次曲线C上的点，且a1=|OP1

(1)若C的方程为+=1,n=3,点P₁(10，0)且S₃=255，求点P₃的坐标；(只需写出一个)

(2)若C的方程为+=1(a＞b＞0)，点P₁(a，0)，对于给定的自然数n，当公差d变化时，求S_n的最小值；

(3)请选定一条除椭圆外的二次曲线C及C上一点P₁，对于给定的自然数n，写出符合条件的点P₁，P₂，…，P_n存在的充要条件，并说明理由.

22.[解] (1) a₁=|OP₁|²=100,

由S₃=(a₁+a₃)=255,得a₃=|OP₃|²=70.

由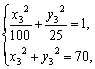解得

∴点P₃的坐标可以为(2，).

(2)[解法一]原点O到二次曲线C：+=1(a＞b＞0)上各点的最小距离为b，最大距离为a.

∵a₁=|OP₁|²=a²,∴d＜0，且a_n=|OP_n|²=a²+(n－1)d≥b².

∴≤d＜0.

∵n≥3,＞0,

∴S_n=na²+d在［,0)上递增.

故S_n的最小值为na²+×=.

[解法二]对每个自然数k(2≤k≤n),

由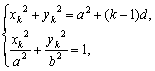

解得y_k²=.

∵0＜y_k²≤b²,得≤d＜0,∴≤d＜0.

以下与解法一相同.

(3)[解法一]若双曲线C：－=1，点P₁(a,0),

则对于给定的n，点P₁，P₂，…，P_n存在的充要条件是d＞0.

∵原点O到双曲线C上各点的距离h∈［|a|,+∞)，且|OP₁|²=a²,

∴点P₁，P₂，…，P_n存在当且仅当|OP_n|²＞|OP₁|²，即d＞0.

[解法二]若抛物线C：y²=2px,点P₁(0,0)，则对于给定的n，

点P₁，P₂，…,P_n存在的充要条件是d＞0.理由同上.

[解法三]若圆C：(x－a)²+y²=a²(a≠0),点P₁(0，0)，

则对于给定的n,点P₁，P₂，…，P_n存在的充要条件是0＜d≤.

∵原点O到圆C上各点的最小距离为0，最大距离为2|a|,且|OP₁|²=0，

∴d＞0且|OP_n|²=(n－1)d≤4a²,

即0＜d≤.