在四棱锥![]() 中,侧面
中,侧面![]() 底面
底面![]() ,
,![]() ,底面
,底面![]() 是直角梯形,
是直角梯形,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
(Ⅰ)求证:![]() 平面
平面![]() ;
;
 (Ⅱ)设
(Ⅱ)设![]() 为侧棱
为侧棱![]() 上异于端点的一点,
上异于端点的一点,![]() ,试确定
,试确定![]() 的值,使得二面角
的值,使得二面角![]() 的大小为
的大小为![]() .
.
在四棱锥![]() 中,侧面
中,侧面![]() 底面
底面![]() ,
,![]() ,底面
,底面![]() 是直角梯形,
是直角梯形,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
(Ⅰ)求证:![]() 平面
平面![]() ;
;
 (Ⅱ)设
(Ⅱ)设![]() 为侧棱
为侧棱![]() 上异于端点的一点,
上异于端点的一点,![]() ,试确定
,试确定![]() 的值,使得二面角
的值,使得二面角![]() 的大小为
的大小为![]() .
.
解析:(Ⅰ)证明:![]() 侧面
侧面![]() 底面
底面![]() 于
于![]() ,
,![]() 面
面![]() ,
,![]() ,
,
![]()
![]() 底面
底面![]() ,
,
![]() 面
面![]()
![]()
![]()
又![]()
![]() ,即
,即![]() ,
,
以![]() 为原点建立空间直角坐标系,则
为原点建立空间直角坐标系,则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,![]()
所以![]() ,所以
,所以![]()
由![]() 底面
底面![]() ,可得
,可得![]() ,
,
又因为![]() ,所以
,所以![]() 平面
平面![]() . ……5分
. ……5分
(Ⅱ)由(Ⅰ)知平面![]() 的一个法向量为
的一个法向量为![]() ,且
,且![]() ,
,![]()
故![]() ,又
,又![]() ,所以
,所以![]() ………………7分
………………7分
设平面![]() 的法向量为
的法向量为![]() ,
,![]()
由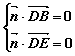 ,得
,得![]() ,取
,取![]()
所以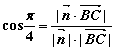 ,………………………………10分
,………………………………10分
解得![]()
![]() ,故
,故![]() …………………………12分
…………………………12分