cosα,I为电灯的光度，b、α如图所示）.
cosα,I为电灯的光度，b、α如图所示）.
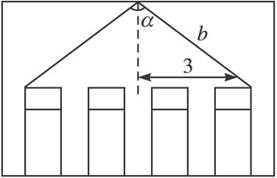
解：
由题设E=
及b=得E=
sin2αcosα要使靠墙的课桌得到最大亮度，即E值最大.∵
是常数，且cosα的值使得（sin2αcosα）2与sin2αcosα同时达到最大值，
因（sin2αcosα）2=cos2α(1-cos2α)2
=
·2cos2α·(1-cos2α)·(1-cos2α),
又由α为锐角，
且2cos2α+(1-cos2α)+(1-cos2α)=2为定值，
∴当2cos2α=1-cos2α，
即cosα=
时（sin2αcosα）2最大.
亦即E最大，这时h=
(米).
注：若x+y+z=k,k为定值，x＞0,y＞0,z＞0,则当且仅当
x=y=z时
xyz有最大值.