е·ІзҹҘеҮҪж•°f(x)пјқcos x(sin xпјӢcos x)пјҚ![]() .
.
(1)иӢҘ0<Оұ<![]() пјҢдё”sin Оұпјқ
пјҢдё”sin Оұпјқ![]() пјҢжұӮf(Оұ)зҡ„еҖјпјӣ
пјҢжұӮf(Оұ)зҡ„еҖјпјӣ
(2)жұӮеҮҪж•°f(x)зҡ„жңҖе°ҸжӯЈе‘ЁжңҹеҸҠеҚ•и°ғйҖ’еўһеҢәй—ҙпјҺ
е·ІзҹҘеҮҪж•°f(x)пјқcos x(sin xпјӢcos x)пјҚ![]() .
.
(1)иӢҘ0<Оұ<![]() пјҢдё”sin Оұпјқ
пјҢдё”sin Оұпјқ![]() пјҢжұӮf(Оұ)зҡ„еҖјпјӣ
пјҢжұӮf(Оұ)зҡ„еҖјпјӣ
(2)жұӮеҮҪж•°f(x)зҡ„жңҖе°ҸжӯЈе‘ЁжңҹеҸҠеҚ•и°ғйҖ’еўһеҢәй—ҙпјҺ
и§Јпјҡж–№жі•дёҖпјҡ(1)еӣ дёә0<Оұ![]() пјҢsin Оұпјқ
пјҢsin Оұпјқ![]() пјҢжүҖд»Ҙcos Оұпјқ
пјҢжүҖд»Ҙcos Оұпјқ![]() .
.
жүҖд»Ҙ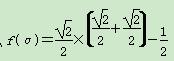
пјқ![]() .
.
(2)еӣ дёәf(x)пјқsin xcos xпјӢcos2xпјҚ![]()
пјқ![]() sin 2xпјӢ
sin 2xпјӢ![]() пјҚ
пјҚ![]()
пјқ![]() sin 2xпјӢ
sin 2xпјӢ![]() cos 2x
cos 2x
 пјқ
пјқ![]() sin 2xпјӢ
sin 2xпјӢ![]() cos 2x
cos 2x
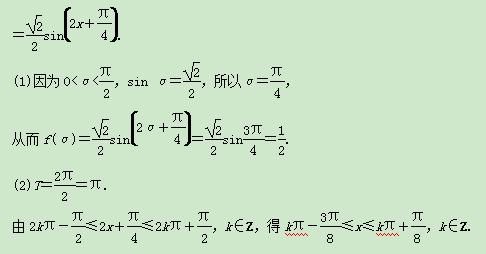 жүҖд»Ҙf(x)зҡ„еҚ•и°ғйҖ’еўһеҢәй—ҙдёә
жүҖд»Ҙf(x)зҡ„еҚ•и°ғйҖ’еўһеҢәй—ҙдёә![]() пјҢkвҲҲZ.
пјҢkвҲҲZ.