如图，四棱柱ABCD﹣A1B1C1D1的底面ABCD是正方形，O为底面中心，A1O⊥平

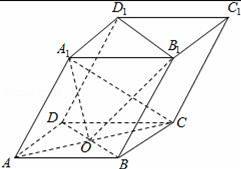
如图，四棱柱ABCD﹣A₁B₁C₁D₁的底面ABCD是正方形，O为底面中心，A₁O⊥平面ABCD，．

（Ⅰ） 证明：A₁C⊥平面BB₁D₁D；

（Ⅱ） 求平面OCB₁与平面BB₁D₁D的夹角θ的大小．

【考点】用空间向量求平面间的夹角；直线与平面垂直的判定；二面角的平面角及求法．

【专题】空间位置关系与距离；空间角．

【分析】（Ⅰ）要证明A₁C⊥平面BB₁D₁D，只要证明A₁C垂直于平面BB₁D₁D内的两条相交直线即可，由已知可证出A₁C⊥BD，取B₁D₁的中点为E₁，通过证明四边形A₁OCE₁为正方形可证A₁C⊥E₁O．由线面垂直的判定定理问题得证．

（Ⅱ）以O为原点，分别以OB，OC，OA₁所在直线为x，y，Z轴建立空间直角坐标系，然后求出平面OCB₁与平面BB₁D₁D的法向量，利用法向量所成的角求平面OCB₁与平面BB₁D₁D的夹角θ的大小．

【解答】（Ⅰ）证明：∵A₁O⊥面ABCD，且BD⊂面ABCD，∴A₁O⊥BD；

又∵在正方形ABCD中，AC⊥BD，A₁O∩AC=O，

∴BD⊥面A₁AC，且A₁C⊂面A₁AC，故A₁C⊥BD．

在正方形ABCD中，∵，∴AO=1，

在Rt△A₁OA中，∵，∴A₁O=1．

设B₁D₁的中点为E₁，则四边形A₁OCE₁为正方形，∴A₁C⊥E₁O．

又BD⊂面BB₁D₁D，且E₁0⊂面BB₁D₁D，且BD∩E₁O=O，

∴A₁C⊥面BB₁D₁D；

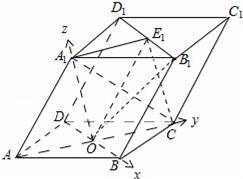
（Ⅱ）解：以O为原点，分别以OB，OC，OA₁所在直线为x，y，Z轴建立如图所示空间直角坐标系，

则B（1，0，0），C（0，1，0），A₁（0，0，1），B₁（1，1，1），

．

由（Ⅰ）知，平面BB₁D₁D的一个法向量，

，．

设平面OCB₁的法向量为，

由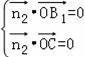，得，取z=﹣1，得x=1．

∴．

则=．

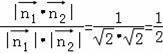
所以，平面OCB₁与平面BB₁D₁D的夹角θ为．

【点评】本题考查了直线与平面垂直的判定，考查了二面角的平面角的求法考查了利用向量求二面角的平面角，解答的关键是建立正确的空间右手系，是中档题．