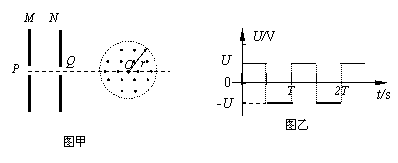
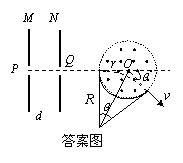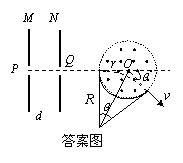（18分）图（甲）所示，一对金属板M和N平行、竖直放置，M、N的中心分别有小孔P、Q，PQ连线垂直金属板。N板右侧有一半径为r的圆形有界的匀强磁场，其圆心O在PQ的延长线上，磁场方向垂直于纸面向外，磁感应强度大小为B。置于P孔附近的粒子源连续不断地沿PQ方向放射出质量为m、电量为＋q的带电粒子（带电粒子所受的重力、初速度及粒子间的相互作用力可忽略），从某一时刻开始，在板M、N间加上如图（乙）所示的交变电压，其周期为T、电压为U，t=0时M板电势高于N板电势。已知带电粒子在M、N两板间一直做加速运动的时间小于T/2，并且只有在每一个周期的前T/4时间内放出的带电粒子才能从小孔Q中射出，求：
（1）带电粒子从小孔Q中射出的最大速度；
（2）M、N两板间的距离；
（3）在沿圆形磁场的边界上，有带电粒子射出的最大弧长。
 |
（1）在M、N电场间处于一直加速的粒子从小孔Q中射出的速度最大，设从最大速度为vm………………1分
根据动能定理
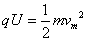………………2分
解得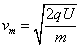 
。………………2分
（2）设M、N两板间距离为d，则两板间的电场强度大小
E=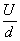
，………………1分
设粒子运动的加速度为a，根据牛顿第二定律 qE=ma………………1分
解得：a=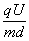
………………1分
每一个周期的第一个T/4时刻放出的带电粒子刚好能从小孔Q中射出，它加速和减速各经历T/4，………………1分
由d=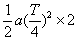
………………2分
解得d=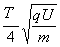
………………1分
（3）每一个周期的前T/4时间内放出的带电粒子才能从小孔Q中射出，其中射出最早的粒子速度最大，越晚射出的粒子速度越小。粒子进入磁场，其中速度越小者运动半径越小，射出点离射入点越近，偏转角度越大（越接近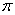
）。最早射入者速度最大，运动半径最大，偏转角度最小，射出点与入射点所夹弧长最大。………………1分
设带电粒子以最大速度射入时在磁场中的运动半径为R，偏转角为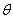
，由牛顿第二定律和几何关系得
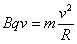………………1分
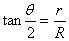………………1分
解得：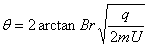
。………………1分
设沿圆形磁场边界上有带电粒子射出的最大弧长为s（图中实线部分），根据弧长公式
s=r(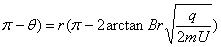
………………2分
