设函数f（x）的定义域为D，若f（x）满足条件：存在[a，b]⊆D，使f（x）在[a，b]上的值域是[
，
]，则成f（x）为“倍缩函数”，若函数f（x）=log2（2x+t）为“倍缩函数”，则t的范围是（ ）
A． （0，
） B． （0，1） C． （0，
] D． （
，+∞]
设函数f（x）的定义域为D，若f（x）满足条件：存在[a，b]⊆D，使f（x）在[a，b]上的值域是[，]，则成f（x）为“倍缩函数”，若函数f（x）=log2（2x+t）为“倍缩函数”，则t的范围是（ ）
A． （0，） B． （0，1） C． （0，] D． （，+∞]
A
考点： 函数的值域．
专题： 新定义．
分析： 由题意得，函数是增函数，构造出方程组，利用方程组的解都大于0，求出t的取值范围．
解答： 解：∵函数f（x）=
为“倍缩函数”，
且满足存在[a，b]⊆D，使f（x）在[a，b]上的值域是[
，
]，
∴f（x）在[a，b]上是增函数；
∴
，
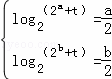即
，
∴方程
+t=0有两个不等的实根，且两根都大于0；
∴
，
解得：0＜t＜
，
∴满足条件t的范围是（0，），
故答案选：A．