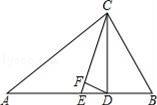
如图，△ABC中，∠A=30°，∠B=70°，CE平分∠ACB，CD⊥AB于D，DF⊥CE，则∠CDF=（ ）
A．20° B．60° C．70° D．80°
如图，△ABC中，∠A=30°，∠B=70°，CE平分∠ACB，CD⊥AB于D，DF⊥CE，则∠CDF=（ ）
A．20° B．60° C．70° D．80°
C．【解答】解：∵∠A+∠B+∠ACB=180°，∠A=30°，∠B=70°，
∴∠ACB=80°，
∵CE平分∠ACB，
∴∠BCE=
∠ACB=
×80°=40°，
∵CD⊥AB，
∴∠CDB=90°，
∵∠B=70°，
∴∠BCD=90°﹣70°=20°，
∴∠FCD=∠BCE﹣∠BCD=20°，
∵DF⊥CE，
∴∠CFD=90°，
∴∠CDF=90°﹣∠FCD=70°．
故选