如果函数y=sin2x+acos2x的图象关于直线x=对称,那么a的值为________________
如果函数y=sin2x+acos2x的图象关于直线x=

对称,那么a的值为__________________.
解法一:正弦函数y=sinx,x∈R的图象的对称轴为直线x=kπ+
(k∈
Z).其对称轴与x轴交点的横坐标即是使函数取得最大值1或最小值-1时的x值.因此,函数y=Asin(ωx+φ)的图象的对称轴可由ωx+φ=kπ+
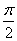
来确定.
∵y=sin2x+acos2x=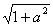
sin(2x+φ)(其中φ由tanφ=a确定),
∴2x+φ=kπ+
(k∈
Z),即φ=kπ+
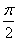
-2x.
将x=
代入,得φ=kπ+

.
故a=tanφ=tan(kπ+
)=-1.
解法二:根据对称轴的定义知,函数图象上到x=
距离相等的x值所对应的函数值相等.令y=f(x)=sin2x+acos2x,则f(x
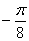
)=f(-x
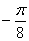
)对任意x都成立.不妨取x=
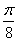
代入,有f(0)=f(-

),
即a=sin(-
)+acos(-
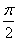
)=-1.
答案:-1
![]()
![]()
![]()
![]()
![]()
![]()
![]()