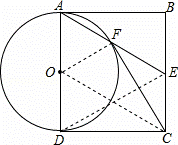
如图，四边形ABCD为矩形，E为BC边中点，连接AE，以AD为直径的⊙O交AE于点F，连接CF．
（1）求证：CF与⊙O相切；
（2）若AD=2，F为AE的中点，求AB的长．
如图，四边形ABCD为矩形，E为BC边中点，连接AE，以AD为直径的⊙O交AE于点F，连接CF．
（1）求证：CF与⊙O相切；
（2）若AD=2，F为AE的中点，求AB的长．
（1）证明：如图所示：连接OF、OC，
∵四边形ABCD是矩形，
∴AD∥BC，AD=BC，∠ADC=90°，
∵E为BC边中点，AO=DO，
∴AO=
AD，EC=BC，
∴AO=EC，AO∥EC，
∴四边形OAEC是平行四边形，
∴AE∥OC，
∴∠DOC=∠OAF，∠FOC=∠OFA，
∵OA=OF，
∴∠OAF=∠OFA，
∴∠DOC=∠FOC，
∵在△ODC和△OFC中
，
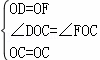∴△ODC≌△OFC（SAS），
∴∠OFC=∠ODC=90°，
∴OF⊥CF，
∴CF与⊙O相切；
（2）解：如图所示：连接DE，
∵AO=DO，AF=EF，AD=2，
∴DE=20F=2，
∵E是BC的中点，
∴EC=1，
在Rt△DCE中，由勾股定理得：
DC=
=
=
，
∴AB=CD=．
