如图,已知AB∥CD∥EF,则x、y、z三者之间的关系是( )
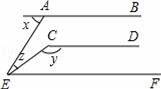

A.x+y+z=180° B.x+y﹣z=180° C.y﹣x﹣z=0° D.y﹣x﹣2z=0°
如图,已知AB∥CD∥EF,则x、y、z三者之间的关系是( )


A.x+y+z=180° B.x+y﹣z=180° C.y﹣x﹣z=0° D.y﹣x﹣2z=0°
B【考点】JA:平行线的性质.
【分析】根据平行线的性质可得∠CEF=180°﹣y,x=z+∠CEF,利用等量代换可得x=z+180°﹣y,再变形即可.
【解答】解:∵CD∥EF,
∴∠C+∠CEF=180°,
∴∠CEF=180°﹣y,
∵AB∥CD,
∴x=z+∠CEF,
∴x=z+180°﹣y,
∴x+y﹣z=180°,
故选:B.
【点评】此题主要考查了平行线的性质,关键是掌握平行线性质定理:
定理1:两条平行线被第三条直线所截,同位角相等. 简单说成:两直线平行,同位角相等.
定理2:两条平行线被地三条直线所截,同旁内角互补..简单说成:两直线平行,同旁内角互补.
定理3:两条平行线被第三条直线所截,内错角相等. 简单说成:两直线平行,内错角相等.