如图，直三棱柱ABC-A1B1C1中，∠ACB=90°，M，N分别为A1B，B1C1的中点．
（1）求证BC∥平面MNB1；
（2）求证平面A1CB⊥平面ACC1A1．
如图，直三棱柱ABC-A1B1C1中，∠ACB=90°，M，N分别为A1B，B1C1的中点．
（1）求证BC∥平面MNB1；
（2）求证平面A1CB⊥平面ACC1A1．
（本小题满分12分）
如图，直三棱柱ABC-A1B1C1中，∠ACB=90°，
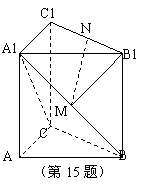M，N分别为A1B，B1C1的中点．
（1）求证BC∥平面MNB1；
（2）求证平面A1CB⊥平面ACC1A1．
答案：（1）因BC∥B1C1， ………………………………………………………………………2分
且B1C1
平面MNB1， …………………………………………………………………………4分
BC
平面MNB1，
故BC∥平面MNB1． …………………………………………………………………………6分
（2）因BC⊥AC，且ABC-A1B1C1为直三棱柱， ……………………………………………8分
故BC⊥平面ACC1A1．
因BC平面A1CB， ……………………………………………………………………………10分
故平面A1CB⊥平面ACC1A1． …………………………………………………………………12分
讲评建议：必修2中的立几初步，必须控制难度，注重答题规范．