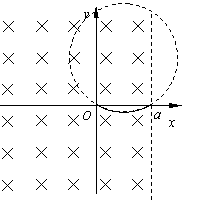
如图所示，在坐标原点有一放射源放出质量为m、带电量为+q的粒子，假设粒子的速率都为v，方向均沿纸面．现在x<a的区域加一垂直于纸面向里的匀强磁场，磁感应强度为
，不计粒子的重力．求：（1）粒子在磁场中运动的最短时间是多少？
（2）为了使粒子不离开磁场，在x=
处放一块与y轴平行的挡板，该挡板能吸收所有打到它上面的粒子，则板的长度至少为多少？
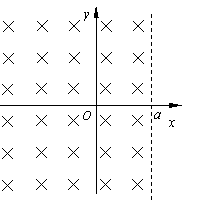
如图所示，在坐标原点有一放射源放出质量为m、带电量为+q的粒子，假设粒子的速率都为v，方向均沿纸面．现在x<a的区域加一垂直于纸面向里的匀强磁场，磁感应强度为，不计粒子的重力．求：（1）粒子在磁场中运动的最短时间是多少？
（2）为了使粒子不离开磁场，在x=处放一块与y轴平行的挡板，该挡板能吸收所有打到它上面的粒子，则板的长度至少为多少？
（1）粒子在磁场中运动，洛伦兹力提供向心力
…………（2分）
得
…………（4分）
如图所示，当粒子从x=a这一点离开磁场时时间最短
…………（4分）
2 1 O y x a
（2）要使粒子不离开磁场，两种临界情况如图所示，
即挡板的最高点为
…………（4分）
最低点为
…………（4分）
所以挡板长度为
d=y1-y2=
…………（4分）
