已知函数![]() (
(![]() )为偶函数.
)为偶函数.
(1)求常数![]() 的值;
的值;
(2)当![]() 取何值时函数
取何值时函数![]() 的值最小?并求出
的值最小?并求出![]() 的最小值;
的最小值;
(3)设![]() (
(![]() ),试根据实数
),试根据实数![]() 的取值,讨论函数
的取值,讨论函数![]() 与
与![]() 的图像的公共点个数.
的图像的公共点个数.
已知函数![]() (
(![]() )为偶函数.
)为偶函数.
(1)求常数![]() 的值;
的值;
(2)当![]() 取何值时函数
取何值时函数![]() 的值最小?并求出
的值最小?并求出![]() 的最小值;
的最小值;
(3)设![]() (
(![]() ),试根据实数
),试根据实数![]() 的取值,讨论函数
的取值,讨论函数![]() 与
与![]() 的图像的公共点个数.
的图像的公共点个数.
解:(1)∵![]() 为偶函数,
为偶函数,
故![]() 对所有
对所有![]() 都成立,--
都成立,-- ![]() 对所有
对所有![]() 都成立,
都成立, ![]()
(2)由(1)得![]() , 即
, 即 ![]()
![]() ,故当且仅当
,故当且仅当![]() 时,-----10分
时,-----10分
![]() 的最小值是
的最小值是![]() .
.
(3)解法1由方程![]() (
(![]() )
)
可变形为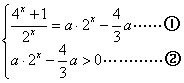 , 由②得
, 由②得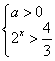 或
或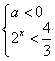 ,
,
由①得![]() ,令
,令![]() ,则
,则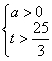 ,或
,或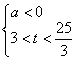
则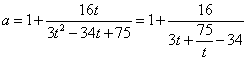 .
.
当![]() 时,
时,![]() 单调递增,∴
单调递增,∴![]() ,
,
∴![]() ,此时方程(
,此时方程(![]() )有且只有一个解; -
)有且只有一个解; -
当![]() 时,
时,![]() ,
,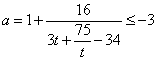
当![]() 时方程(
时方程(![]() )有且只有一个解;
)有且只有一个解;
当![]() 时,方程(
时,方程(![]() )有两解;
)有两解;
当![]() ,或
,或![]() 时方程(
时方程(![]() )无解.
)无解.
综上所述,当![]() 时,函数
时,函数![]() 与
与![]() 的图像有两个不同的公共点;
的图像有两个不同的公共点;
当![]() 或
或![]() 时,函数
时,函数![]() 与
与![]() 的图像有且只有一个公共点;
的图像有且只有一个公共点;
当![]() 或
或![]() 时,函数
时,函数![]() 与
与![]() 的图像没有公共点. -
的图像没有公共点. -
[解法2: ![]() (
(![]() )
) 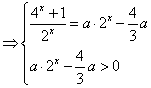
![]()
![]() --
-- 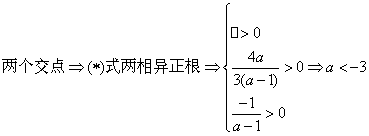
![]()
![]()
![]() ,
,![]() ,
,
![]() .
.