将一块直角三角板ABO置于平面直角坐标系中（如图所示）.已知AB=OB=1，AB⊥OB，点P
是三角板内一点.现因三角板中阴影部分受到损坏，要把损坏部分锯掉，可用经过点P的任一直线MN将三角板锯成△AMN.问应如何确定直线MN的斜率，可使锯成的△AMN的面积最大？
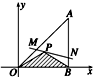
将一块直角三角板ABO置于平面直角坐标系中（如图所示）.已知AB=OB=1，AB⊥OB，点P 是三角板内一点.现因三角板中阴影部分受到损坏，要把损坏部分锯掉，可用经过点P的任一直线MN将三角板锯成△AMN.问应如何确定直线MN的斜率，可使锯成的△AMN的面积最大？
当斜率为-
时，S△AMN(max)=
由题意可知B（1，0），A（1，1），
kOP=，kPB=-，
∴kMN∈
，lAO：y=x；lAB：x=1.
设lMN：y=kx+b，
∵直线MN过P
∴b=
k，∴y=kx+
.
∴M
,N
S△AMN=
×
设t=1-k∈
.
S△AMN=
在t∈时，函数单调递增.
∴当t=
，即k=-时，S△AMN(max)=.