 (吨)时,超过部分每吨加收环境保护费
(吨)时,超过部分每吨加收环境保护费 元.下图反映了每月收取的水费
元.下图反映了每月收取的水费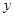 (元)与每月用水量
(元)与每月用水量 (吨)之间的函数关系.
(吨)之间的函数关系.请你解答下列问题:
【小题1】将m看作已知量,分别写出当0<x<m和x>m时,
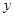 与
与 之间的函数关系式;
之间的函数关系式;【小题2】按上述方案,一家酒店四、五两月用水量及缴费情况如下表所示,那么,这家酒店四、五两月的水费分别是按哪种方案计算的?并求出
 的值.
的值.| 月份 | 用水量 (吨) (吨) | 水费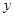 (元) (元) |
| 四月 | 35 | 59.5 |
| 五月 | 80 | 151 |
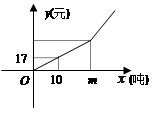
 (吨)时,超过部分每吨加收环境保护费
(吨)时,超过部分每吨加收环境保护费 元.下图反映了每月收取的水费
元.下图反映了每月收取的水费 (元)与每月用水量
(元)与每月用水量 (吨)之间的函数关系.
(吨)之间的函数关系. 与
与 之间的函数关系式;
之间的函数关系式; 的值.
的值.| 月份 | 用水量 (吨) (吨) | 水费 (元) (元) |
| 四月 | 35 | 59.5 |
| 五月 | 80 | 151 |
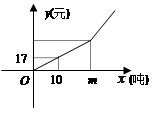
 或
或 ( x≥m) ;
( x≥m) ; 来计算的)
来计算的)