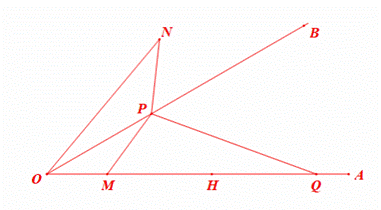
已知
，H为射线OA上一定点，
，P为射线OB上一点，M为线段OH上一动点，连接PM，满足
为钝角，以点P为中心，将线段PM顺时针旋转
，得到线段PN，连接ON．
（1）依题意补全图1；
（2）求证：
；
（3）点M关于点H的对称点为Q，连接QP．写出一个OP的值，使得对于任意的点M总有ON=QP，并证明．
已知，H为射线OA上一定点，，P为射线OB上一点，M为线段OH上一动点，连接PM，满足为钝角，以点P为中心，将线段PM顺时针旋转，得到线段PN，连接ON．
（1）依题意补全图1；
（2）求证：；
（3）点M关于点H的对称点为Q，连接QP．写出一个OP的值，使得对于任意的点M总有ON=QP，并证明．
解析】
（1）如图所示
（2）在△OPM中，∠OMP=180°-∠POM-∠OPM=150°-∠OPM
∠OPN=∠MPN-∠OPM=150°-∠OPM
∴∠OMP=∠OPN
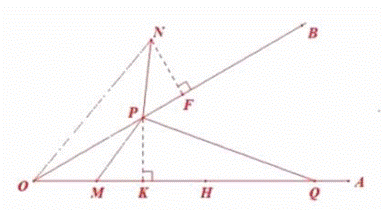
（3）过点P作PK⊥OA，过点N作NF⊥OB.
∵∠OMP=∠OPN，∴∠PMK=∠NPF
在△NPF和△PMK中
，∴△NPF≌△PMK（AAS）
∴PF=MK，∠PNF=∠MPK，NF=PK.
又∵ON=PQ，在Rt△NOF和Rt△PKQ中
，∴Rt△NOF≌Rt△PKQ（HL），∴KQ=OF.
设MK=y，PK=x
∵∠POA=30°，PK⊥OQ
∴OP=2x，∴OK=
，
∴
，
∵M与Q关于H对称，∴MH=HQ
∴KQ=KH+HQ=
∵KQ=OF，∴
，整理得
所以
，即PK=1
∵∠POA=30°，∴OP=2