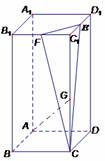
（14分）在正四棱柱
中，E,F分别是
的中点，G为
上任一点，EC与底面ABCD所成角的正切值是4.
（Ⅰ）求证AG
EF；
（Ⅱ）确定点G的位置，使AG面CEF,并说明理由；
（Ⅲ）求二面角
的余弦值。
（14分）在正四棱柱中，E,F分别是的中点，G为上任一点，EC与底面ABCD所成角的正切值是4.
（Ⅰ）求证AGEF；
（Ⅱ）确定点G的位置，使AG面CEF,并说明理由；
（Ⅲ）求二面角的余弦值。
（14分）
解：∵
是正四棱柱
∴ABCD是正方形，设其边长为2a,ÐECD是EC与底面所成的角。而ÐECD=ÐCEC1, ∴CC1=4EC1=4a.……………1分
以A为原点，AB、AD、AA1所在的直线分别为x轴,y轴,z轴，建立如图所示的直角坐标系。
则A(0,0,0),B(2a,0,0),C(2a,2a,0),D(0,2a,0),
A1(0,0,4a),B1(2a,0,4a),C1(2a,2a,4a),D1(0,2a,4a),
E(a,2a,4a),F(2a,a,4a),设G(2a,2a,b)(0<b<4a)………………3分
（Ⅰ）
=（2a,2a,b）,
=(a,-a,0),
=2a2-2a2+0=0,
∴AG
EF ……………………………………………………6分
（Ⅱ）由（Ⅰ）知，使AG面CEF，只需AGCE,
只需
=（2a,2a,b）×（-a,0,4a）=-2a2+4ab=0,
∴b=
a,即CG=
CC1时，AG面CEF。………………10分
（Ⅲ）由（Ⅱ）知，当G(2a,2a, a)时，是平面CEF的一个法向量，
由题意可得，
是平面CEC1的一个法向量，
设二面角
的大小为q，
则cosq=
=
=
,
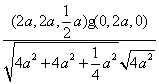二面角的余弦值为. …………………………14分
（运用综合法相应给分）