设
与
是两个单位向量，其夹角为60°，且
=2+，
=﹣3+2．
（1）求•；
（2）求||和||；
（3）求与
的夹角．
设与是两个单位向量，其夹角为60°，且=2+，=﹣3+2．
（1）求•；
（2）求||和||；
（3）求与的夹角．
考点： 平面向量数量积的运算．
专题： 计算题；平面向量及应用．
分析： （1）运用向量的数量积的定义和向量的平方即为模的平方，计算即可得到；
（2）运用向量的平方即为模的平方，计算即可得到；
（3）运用向量的夹角公式和夹角的范围，计算即可得到所求值．
解答： 解：（1）由
与
是两个单位向量，其夹角为60°，
则
=1×
=
，
=（2
+
）•（﹣3+2）=﹣6
+2
+•
=﹣6+2+
=﹣
；
（2）|
|=
=
=
=
，
|
|=
=
=
=；
（3）cos＜
，
＞=
=
=﹣
，
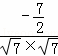由于0≤＜，＞≤π，
则有与的夹角
．
点评： 本题考查平面向量的数量积的定义和性质，考查向量的平方即为模的平方，考查向量的夹角公式的运用，考查运算能力，属于基础题．