如图,正方形ABCD中,点E在对角线AC上,连接EB、ED.
(1)求证:△BCE≌△DCE;
(2)延长BE交AD于点F,若∠DEB=140º,求∠AFE的度数.
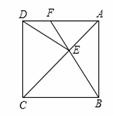
如图,正方形ABCD中,点E在对角线AC上,连接EB、ED.
(1)求证:△BCE≌△DCE;
(2)延长BE交AD于点F,若∠DEB=140º,求∠AFE的度数.

(1)证明:∵正方形ABCD中,E为对角线AC上一点,
∴BC=DC,∠BCE=∠DCE=45º
又∵CE=CE ∴△BCE≌△DCE(SAS)
(2)解:由全等可知,∠BEC=∠DEC=![]() ∠DEB=
∠DEB=![]() ×140º=70º 在△BCE中,∠CBE=180º—70º—45º=65º
×140º=70º 在△BCE中,∠CBE=180º—70º—45º=65º
∴在正方形ABCD中,AD∥BC,有∠AFE=∠CBE=65º