a，点P到平面ABC的距离为
a.
(Ⅰ)求证：平面PBC⊥平面ABC；
(Ⅱ)求二面角P-AC-B的大小；
(Ⅲ)求点B到平面PAC的距离.
a，点P到平面ABC的距离为a.
(Ⅰ)求证：平面PBC⊥平面ABC；
(Ⅱ)求二面角P-AC-B的大小；
(Ⅲ)求点B到平面PAC的距离.
答案：
(I)由已知,△ABC为Rt△,∠BAC=90°.
∵PA=PB=PC.∴点P在平面ABC上的射影是斜线BC的中点E.
∴平面PBC⊥平面ABC；
(Ⅱ)取AC的中点,D,连接PD、PE、DE.
∵PE⊥平面ABC,DE上AC于D,(DE∥AB)
∴AC上PD.∴∠PDE为二面角P—AC—B的平面角.
∴tan∠PDE=.∵∠PDE=60°.
故二面角P-AC-B为60°.
(Ⅲ)∵PD=S△PAC=
.
设点B到平面PAC的距离为d.由VF-ABC=VB-PAC
得
S△ABC·PE=
S△PAC·d.
∴
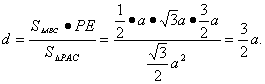
(也可以用向理法求解,略).