设函数f(x)=a·b,其中向量a=(m,cosx),b=(1+sinx,1),x∈R,且f()=2.(1)求实数m的
设函数f(x)=
a·
b,其中向量
a=(m,cosx),
b=(1+sinx,1),
x∈R,且f(
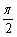
)=2.
(1)求实数m的值;
(2)求函数f(x)的最小值.
解:(1)f(x)=
a·
b=m(1+sinx)+cosx,f(
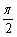
)=m(1+sin
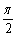
)+cos
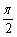
=2,得m=1.
(2)由(1),得f(x)=sinx+cosx+1= sin(x+
sin(x+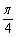 )+1,
)+1,
∴当sin(x+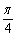 )=-1时,f(x)的最小值为1-
)=-1时,f(x)的最小值为1-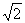 .
.
![]() sin(x+
sin(x+![]() )+1,
)+1,![]() )=-1时,f(x)的最小值为1-
)=-1时,f(x)的最小值为1-![]() .
.