如图，在矩形ABCD中，AB=8，AD=12，过点A、D两点的⊙O与BC边相切于点E，则⊙O的半径为 ．
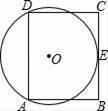
如图，在矩形ABCD中，AB=8，AD=12，过点A、D两点的⊙O与BC边相切于点E，则⊙O的半径为 ．
．
【考点】MC：切线的性质；LB：矩形的性质．
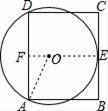
【分析】连结EO并延长交AD于F，如图，由切线的性质得OE⊥BC，再利用平行线的性质得到OF⊥AD，则根据垂径定理得到AF=DF=
AD=6，易得四边形ABEF为矩形，则EF=AB=8，设⊙O的半径为r，则OA=r，OF=8﹣r，然后在Rt△AOF中利用勾股定理得到（8﹣r）2+62=r2，再解方程求出r即可．
【解答】解：连结EO并延长交AD于F，如图，
∵⊙O与BC边相切于点E，
∴OE⊥BC，
∵四边形ABCD为矩形，
∴BC∥AD，
∴OF⊥AD，
∴AF=DF=AD=6，
易得四边形ABEF为矩形，则EF=AB=8，设⊙O的半径为r，则OA=r，OF=8﹣r，
在Rt△AOF中，∵OF2+AF2=OA2，
∴（8﹣r）2+62=r2，解得r=
，
即⊙O的半径为．
故答案为．
【点评】本题考查了切线的性质：圆的切线垂直于经过切点的半径；若出现圆的切线，必连过切点的半径，构造定理图，得出垂直关系．也考查了垂径定理和矩形的性质．解决本题的关键是构建直角三角形，利用勾股定理建立关于半径的方程．