设F(1,0)是抛物线G:y2=2px的焦点.（Ⅰ）求抛物线及准线方程;
（Ⅱ）求过点P（0，-2）与抛物线G有一个公共点的直线方程；
（III）若点P是抛物线上的动点，点P在y轴上的射影是Q，点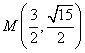
，试判断
是否存在最小值，若存在求出其最小值，若不存在，请说明理由;
设F(1,0)是抛物线G:y2=2px的焦点.（Ⅰ）求抛物线及准线方程;
（Ⅱ）求过点P（0，-2）与抛物线G有一个公共点的直线方程；
（III）若点P是抛物线上的动点，点P在y轴上的射影是Q，点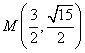，试判断是否存在最小值，若存在求出其最小值，若不存在，请说明理由;
解：（Ⅰ）抛物线方程: y2=4x, 准线方程:x=-1. <1分>
（Ⅱ）当斜率不存在时：直线L：x=0与抛物线相切；
设直线L：y+2=kx与抛物线G有一个公共点:
消y得:
<2分>
∴当k=0时直线L与抛物线G有一个交点；<3分>
当k
=0时：
，解得：k=-
, <4分>
∴所求直线方程：x=0或y=-2或y=-
x-2. <5分>
（III）易知点A在抛物线的外侧，延长PM交直线
，
由抛物线的定义可知
,
当三点
共线时，
最小，此时为
，
又焦点坐标为
,所以
，
即
的最小值为
，所以
的最小值为1 。