已知直角坐标系中菱形ABCD的位置如图，C，D两点的坐标分别为(4,0)，(

已知直角坐标系中菱形ABCD的位置如图，C，D两点的坐标分别为(4,0)，(0,3).现有两动点P,Q分别从A,C同时出发，点P沿线段AD向终点D运动，点Q沿折线CBA向终点A运动，设运动时间为t秒.

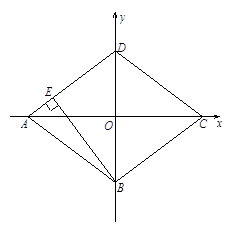
1.填空：菱形ABCD的边长是  ▲  、面积是  ▲  、 高BE的长是  ▲  ；

2.探究下列问题：

①若点P的速度为每秒1个单位，点Q的速度为每秒2个单位.当点Q在线段BA上时，求△APQ的面积S关于t的函数关系式，以及S的最大值；

②若点P的速度为每秒1个单位，点Q的速度变为每秒k个单位，在运动过程中,任何时刻都有相应的k值，使得△APQ沿它的一边翻折，翻折前后两个三角形组成的四边形为菱形.请探究当t = 4 秒时的情形，并求出k的值.

1.5, 24,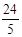

2.①由题意，得AP=t，AQ=10-2t.

如图1,过点Q作QG⊥AD，垂足为G，由QG∥BE得

△AQG∽△ABE,∴,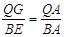

∴QG=,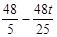

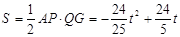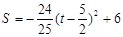∴(≤t≤5).

∵(≤t≤5).

∴当t=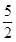时，S最大值为6.

② 要使△APQ沿它的一边翻折，翻折前后的两个三角形组

成的四边形为菱形，根据轴对称的性质，只需△APQ为等腰三角形即可.

当t=4秒时，∵点P的速度为每秒1个单位，∴AP=.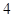

以下分两种情况讨论:

第一种情况：当点Q在CB上时, ∵PQ≥BE>PA，∴只存在点Q₁,使Q₁A=Q₁P.

如图2,过点Q₁作Q₁M⊥AP，垂足为点M，Q₁M交 AC于点F,则AM=.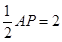

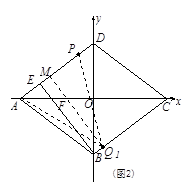
由△AMF∽△AOD∽△CQ₁F,得

, ∴,

∴.

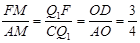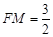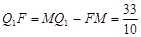∴CQ₁=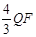=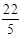.则,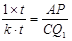

∴ 

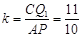
第二种情况：当点Q在BA上时,存在两点Q₂,Q₃,分别使A P= A Q₂,PA=PQ₃.

①  若AP=AQ₂，如图3,CB+BQ₂=10-4=6.

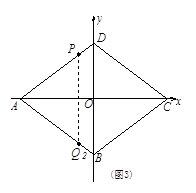
则,∴.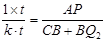

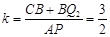②若PA=PQ₃，如图4,过点P作PN⊥AB，垂足为N，

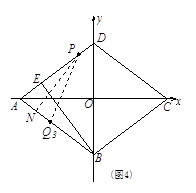
由△ANP∽△AEB,得.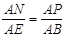

∵AE=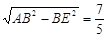 ,∴AN＝.

∴AQ₃=2AN=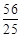,  ∴BC+BQ₃=10-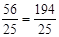

则.∴.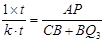

综上所述，当t= 4秒，以所得的等腰三角形APQ沿底边翻折，

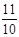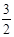翻折后得到菱形的k值为或或.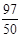

 解析:略
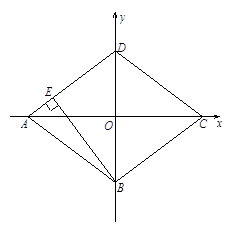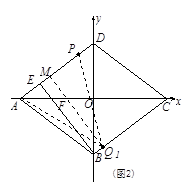
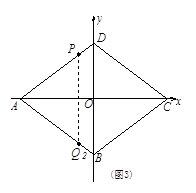
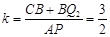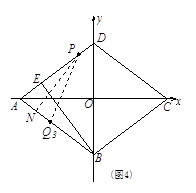