设A＝{x|x2
2(a1)xa2
1＝0}，
，x∈Z}．
若A∩B＝A，求a的取值范围．
设A＝{x|x22(a1)xa21＝0}，，x∈Z}．
若A∩B＝A，求a的取值范围．
．
【解析】由，x∈Z}，得
．
由A∩B＝A，得A⊆B．于是，A有四种可能，
即
，
，A＝{0}，
．
以下对A分类讨论：
（1）若，则Δ＝4(a1)24a24＝8a8<0，解得a<1；
（2）若，则Δ＝8a8＝0，解得a＝1．
此时x22(a1)xa21＝0可化为x2＝0，
所以x＝0，这与x＝4是矛盾的；
（3）若A＝{0}，则由（2）可知，a＝1；
（4）若A＝{4，0}，则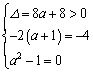
，解得a＝1．
综上可知，a的取值范围．