(本小题共12分)数列![]() 满足
满足![]() ,(
,(![]() )
)
(Ⅰ) 当![]() 时,求
时,求![]() 及
及![]() ;
;
(Ⅱ)是否存在实数![]() ,使得数列
,使得数列![]() 为等差数列或等比数列?若存在,求出其通项公式,若不存在,说明理由;
为等差数列或等比数列?若存在,求出其通项公式,若不存在,说明理由;
(本小题共12分)数列![]() 满足
满足![]() ,(
,(![]() )
)
(Ⅰ) 当![]() 时,求
时,求![]() 及
及![]() ;
;
(Ⅱ)是否存在实数![]() ,使得数列
,使得数列![]() 为等差数列或等比数列?若存在,求出其通项公式,若不存在,说明理由;
为等差数列或等比数列?若存在,求出其通项公式,若不存在,说明理由;
解:(本小题共12分)(Ⅰ) ![]()
![]() ,故
,故![]() ,所以
,所以![]() .
.
(Ⅱ) ![]() ,
,
![]() ,
,
![]() ,
,
若数列![]() 为等差数列,则
为等差数列,则![]()
![]() 方程没有实根,故不存在
方程没有实根,故不存在![]() ,使得数列
,使得数列![]() 为等差数列.
为等差数列.
若数列![]() 为等比数列,则
为等比数列,则![]() ,即
,即![]()
解得:![]() .
.![]()
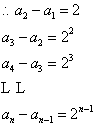 将
将![]() 个式子相加,
个式子相加,![]() ,
,
![]()
![]()
又![]() 符合条件,
符合条件,![]()
![]()
![]() ,故数列
,故数列![]() 为等比数列.通项公式为
为等比数列.通项公式为![]()