首页 / 正三棱柱ABC—A1B1C1的底面边长为a,在侧棱BB1上截取BD=,在侧棱CC1上截取

正三棱柱ABC—A1B1C1的底面边长为a,在侧棱BB1上截取BD=,在侧棱CC1上截取

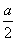
正三棱柱ABC—A1B1C1的底面边长为a,在侧棱BB1上截取BD=,在侧棱CC1上截取CE=a,过A,D,E作棱柱的截面.求证:截面ADE⊥侧面ACC1A1.

答案

证明：取BC的中点O,如图建立空间直角坐标系.

则A(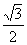

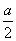
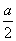
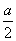
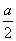
a,0,0),B(0,a2,0),D(0,,),E(0,-,a),C(0,-,0).

所以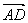

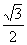
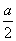
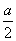
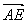
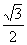
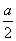
=(-a,,),=(-a,-,a).

设平面ADE的法向量为n1=(x1,y1,z1),则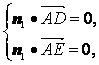

所以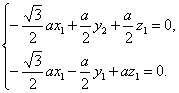

令y1=1,则n1=(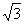

,1,2).

又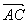

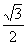
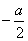
=(-a,,0).

设平面ACC1A1的法向量为n2=(x2,y2,z2).

所以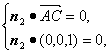

所以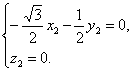

令x2=1,则n2=(1,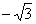

,0).

所以n1·n2=0.所以n1⊥n2.

所以截面ADE⊥侧面ACC1A1.


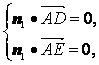
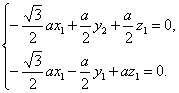
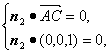
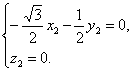
相关题目

已知n是大于1的自然数，求证：2n＞1+.
已知n是大于1的自然数，求证：2n＞1+.
下列句子中，没有语病的一项是( ) A．在北京、天津、上海
下列句子中，没有语病的一项是( ) A．在北京、天津、上海举办的前3届世乒赛鉴于均由党和国家领导人出席并宣布开幕和闭幕，因此，2008年广州第49届
△ABC中，D、E分别是边AB与AC的中点，BC=4，下面四个结论：①D
△ABC中，D、E分别是边AB与AC的中点，BC=4，下面四个结论：①DE=2；②△ADE∽△ABC；③△ADE的面积与△ABC的面积之比为 1：4；④△ADE的周长与△ABC的周长之
为了保持果树的优良特性，加快果树的繁殖速度，果农通常
为了保持果树的优良特性，加快果树的繁殖速度，果农通常不采用的繁殖方法是（ ） A．嫁接繁殖B．种子繁殖C．扦插繁殖D．压条繁殖
下列关于人体内环境稳态的叙述中，错误的是（ ） A．细胞
下列关于人体内环境稳态的叙述中，错误的是（ ） A．细胞外液渗透压降低时，抗利尿激素分泌量减少 B．组织液渗回血浆或渗入淋巴受阻会导致组织
下图是小明在研究性学习中使用的一幅地图。根据地图所示
下图是小明在研究性学习中使用的一幅地图。根据地图所示内容判断，小明研究的课题是 A．新航路开辟           B．丝绸之路            
3．依次填入下面一段文字横线处的语句，衔接最恰当的一组
3．依次填入下面一段文字横线处的语句，衔接最恰当的一组是 （  ） “家”作为社会关系的核心，    。      ，        ，      。     
某研究性学习小组请你参与“研究铁与水反应所得固体物质
某研究性学习小组请你参与“研究铁与水反应所得固体物质的成分、性质及再利用”实验探究，并共同解答下列问题： 探究一 设计如图所示装置进行“

最新题目

如图所示，质量为m=4kg的物体与水平地面间的动摩擦因数μ=0.2
某高等生物细胞用纤维素酶处理有反应且能利用CO2合成有机
欧洲航天局用阿里亚娜火箭发射地球同步卫星。该卫星发射
Do you know the year _____Einstein died?A. when              B. at
“绝圣弃智，民利百倍；绝仁弃义，民复孝兹；绝巧弃利，
植物细胞对矿质离子的吸收，之所以具有选择性是与     
– Would you like to go to the cinema tonight? -- I’d like ______, but I am t
There is ________ “h” and ________ “u” in the word “house”. A. a; a
到三角形的三边距离相等的点是 （      ）。 A、三条角
在一次测玻璃的折射率实验中，采用了如下方法，将一块半
对下列句子中加点的词解释不正确的一项是 Ａ.逮奉圣朝（
如图5所示，固定在水平面上的光滑半球，球心O的正上方固定
已知平面区域恰好被面积最小的圆及其内部所覆盖．（1）试
现代医学认为，任何与人体生理不适应的环境和事件都称为
下列各组物质制成的无色透明液体，能通过丁达尔现象鉴别
第二次世界大战后，在日本广岛生活的人癌症发病率很高，
已知某纯碱试样中含有杂质氯化钠，为测定试样中纯碱的质
如图为物质跨膜运输示意图(甲、乙、丙代表物质，a,b,c,d,e代
小华在解一元二次方程时，只得出一个根x=1，则被漏掉的一
下列词语加点的词，注音全都正确的一组是（    ） A．媲(p