如图，半径R=0.4m的圆盘水平放置，绕竖直轴OO′匀速转动，在圆心O正上方h=0.8m高处固定一水平轨道PQ，转轴和水平轨道交于O′点。一质量m=1kg的小车（可视为质点），在F=4N的水平恒力作用下，从O′左侧x0=2m处由静止开始沿轨道向右运动，当小车运动到O′点时，从小车上自由释放一小球，此时圆盘半径OA与x轴重合。规定经过O点水平向右为x轴正方向。小车与轨道间的动摩擦因数μ=0.2，g取10m/s2。
⑴若小球刚好落到A点，求小车运动到O′点的速度；
⑵为使小球刚好落在A点，圆盘转动的角速度应为多大？
⑶为使小球能落到圆盘上，求水平拉力F作用的距离范围。
 |
（1）小球离开小车后，由于惯性，将以离开小车时的速度作平抛运动，
小车运动到
点的速度 
m/s （2分）
（2）为使小球刚好落在A点，则小球下落的时间为圆盘转动周期的整数倍，有
，其中k = 1,2,3,…… （1分）
即
rad/s，其中k = 1,2,3…… （1分）
（3）小球若能落到圆盘上，其在O′点的速度范围是：0<v≤1m/s ，设水平拉力作用的最小距离与最大距离分别为x1、x2，对应到达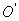
点的速度分别为0、1m/s。
代入数据解得 
m （2分）
代入数据解得 
m或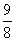
m （2分）
则水平拉力F作用的距离范围 1m < x ≤1.125m （1分）
（直接用功能关系计算同样给分）