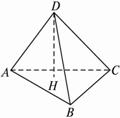
(1)求证:BD⊥平面ADC;
(2)若H是△ABC的垂心,求证:H是D在平面ABC内的射影.

(1)求证:BD⊥平面ADC;
(2)若H是△ABC的垂心,求证:H是D在平面ABC内的射影.
证明:(1)∵BD⊥AD,BD⊥DC,AD∩DC=D,∴BD⊥面ADC.

(2)由(1)知BD⊥AC.
∵AD=BD=CD,∠ADB=∠BDC=90°,∴AB=AC.
又∵∠BAC=60°,
∴△ABC为等边三角形.
∴AB=BC=AC.
∴可得∠ADC=90°.
同理可证AD⊥面BCD![]() AD⊥BC.
AD⊥BC.
∴![]() .
.
∴![]() .
.
∴![]() =0.
=0.
∴DH⊥面ABC.
∴H是D在面ABC内的射影.