(14分)
如图, ABCD为矩形,CF⊥平面ABCD,DE⊥平面ABCD,
AB=4a,BC= CF=2a, P为AB的中点.
(1)求证:平面PCF⊥平面PDE;
(2)求四面体PCEF的体积.
(14分)
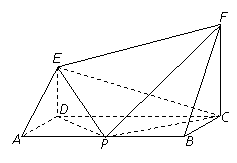
如图, ABCD为矩形,CF⊥平面ABCD,DE⊥平面ABCD,
AB=4a,BC= CF=2a, P为AB的中点.
(1)求证:平面PCF⊥平面PDE;
(2)求四面体PCEF的体积.

证明:
(1)因为ABCD为矩形,AB=2BC, P为AB的中点,
所以三角形PBC为等腰直角三角形,∠BPC=45°. …………………………2分
同理可证∠APD=45°.
所以∠DPC=90°,即PC⊥PD. …………………………3分
又DE⊥平面ABCD,PC在平面ABCD内,所以PC⊥DE. ………………………4分
因为DE∩PD=D ,所以PC ⊥PDE . …………………………5分
又因为PC在平面PCF内,所以平面PCF⊥平面PDE. …………………………7分
【解】(2)因为CF⊥平面ABCD,DE⊥平面ABCD,
所以DE//CF. 又DC⊥CF,
所以![]() ……………………… 10分
……………………… 10分
在平面ABCD内,过P作PQ⊥CD于Q,则
PQ//BC,PQ=BC=2a.
因为BC⊥CD,BC⊥CF,
所以BC⊥平面PCEF,即PQ⊥平面PCEF,
亦即P到平面PCEF的距离为PQ=2a. ………………………12分
![]() ………………………14分
………………………14分
(注:本题亦可利用![]() 求得)
求得)