如图,P—ABCD是正四棱锥,ABCD—A1B1C1D1是正方体,其中AB=2,PA= 
.
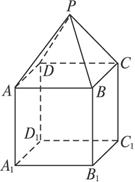
(1)求证:PA⊥B1D1;
(2)求平面PAD与平面BDD1B1所成的锐二面角的大小;
(3)求B1到平面PAD的距离.
如图,P—ABCD是正四棱锥,ABCD—A1B1C1D1是正方体,其中AB=2,PA= .
(1)求证:PA⊥B1D1;
(2)求平面PAD与平面BDD1B1所成的锐二面角的大小;
(3)求B1到平面PAD的距离.
解法一:(1)以D1为原点,D1A1为x轴,D1C1为y轴,DD1为z轴建立空间直角坐标系,D1(0,0,0),A1(2,0,0),B1(2,2,0),C1(0,2,0),D(0,0,2),A(2,0,2),B(2,2,2),C(0,2,2),P(1,1,4).
∵
=(-1,1,2),=(2,2,0),
∴
·
=0,
即PA⊥D1B1.
(2)平面BDD1B1的法向量为
=(-2,2,0),
=(2,0,0),
=(1,1,2),
设平面PAD的法向量为n
=(x,y,z),则n⊥
且n⊥
,∴
取n=(0,2,-1),
设所求的锐二面角为θ,则
cosθ=|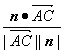
|=
,
θ=arccos
.
(3)
=(2,2,-2),设所求的距离为d,
则d=|
|=
.
解法二:(1)连结AC,交BD于点O,连结PO,则PO⊥平面ABCD.
又∵AC⊥BD,∴PA⊥BD.
∵BD∥B1D1,∴PA⊥B1D1.
(2)∵AO⊥BD,∴AO⊥PO.∴AO⊥平面PBD.
过点O作OM⊥PD于点M,连结AM,则AM⊥PD.
∴∠AMO就是二面角APDO的平面角.
∵AB=2,PA=
,
∴AO=
,PO=
=2,OM=
=
=
.
∴tan∠AMO=
,
即二面角的大小为arctan
.
(3)用体积法求解:连结B1P,B1D,B1A,
则
h·S△PAD=
AO·
,
即有
h·
·2·
=
·
·
·
,
解得h=
,即B1到平面PAD的距离为
.