(本小题满分14分)
已知点![]() 在抛物线
在抛物线![]()
![]() 上,
上,![]() 点到抛物线
点到抛物线![]() 的焦点F的距离为2,
的焦点F的距离为2,
直线![]()
![]() 与抛物线交于
与抛物线交于![]() 两点.
两点.
(Ⅰ)求抛物线![]() 的方程;
的方程;
(Ⅱ)若以![]() 为直径的圆与
为直径的圆与![]() 轴相切,求该圆的方程;
轴相切,求该圆的方程;
(Ⅲ)若直线![]() 与
与![]() 轴负半轴相交,求
轴负半轴相交,求![]() 面积的最大值.
面积的最大值.
(本小题满分14分)
已知点![]() 在抛物线
在抛物线![]()
![]() 上,
上,![]() 点到抛物线
点到抛物线![]() 的焦点F的距离为2,
的焦点F的距离为2,
直线![]()
![]() 与抛物线交于
与抛物线交于![]() 两点.
两点.
(Ⅰ)求抛物线![]() 的方程;
的方程;
(Ⅱ)若以![]() 为直径的圆与
为直径的圆与![]() 轴相切,求该圆的方程;
轴相切,求该圆的方程;
(Ⅲ)若直线![]() 与
与![]() 轴负半轴相交,求
轴负半轴相交,求![]() 面积的最大值.
面积的最大值.
【解析】(Ⅰ)抛物线![]()
![]() 的准线为
的准线为![]() , ................1分
, ................1分
由抛物线定义和已知条件可知![]() ,
,
解得![]() ,故所求抛物线方程为
,故所求抛物线方程为![]() . .............................3分
. .............................3分
(Ⅱ)联立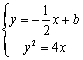 ,消
,消![]() 并化简整理得
并化简整理得![]() .
.
依题意应有![]() ,解得
,解得![]() . ............................4分
. ............................4分
设![]() ,则
,则![]() , ..............................5分
, ..............................5分
设圆心![]() ,则应有
,则应有![]() .
.
因为以![]() 为直径的圆与
为直径的圆与![]() 轴相切,得到圆半径为
轴相切,得到圆半径为![]() , ...............6分
, ...............6分
又![]() .
.
所以 ![]() , .....................7分
, .....................7分
解得![]() . .........................8分
. .........................8分
所以![]() ,所以圆心为
,所以圆心为![]() .
.
故所求圆的方程为![]() . .......................9分
. .......................9分
方法二:
联立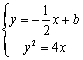 ,消掉
,消掉![]() 并化简整理得
并化简整理得![]() ,
,
依题意应有![]() ,解得
,解得![]() . ........................4分
. ........................4分
设![]() ,则
,则![]() . ........................5分
. ........................5分
设圆心![]() ,则应有
,则应有![]() ,
,
因为以![]() 为直径的圆与
为直径的圆与![]() 轴相切,得到圆半径为
轴相切,得到圆半径为![]() . ......................6分
. ......................6分
又![]() ,
,
又![]() ,所以有
,所以有![]() , ...............................7分
, ...............................7分
解得![]() , .................8分
, .................8分
所以![]() ,所以圆心为
,所以圆心为![]() .
.
故所求圆的方程为![]() . ...................9分
. ...................9分
(Ⅲ)因为直线![]() 与
与![]() 轴负半轴相交,所以
轴负半轴相交,所以![]() ,
,
又![]() 与抛物线交于两点,由(Ⅱ)知
与抛物线交于两点,由(Ⅱ)知![]() ,所以
,所以![]() ,.........................10分
,.........................10分
直线![]() :
:![]() 整理得
整理得![]() ,
,
点![]() 到直线
到直线![]() 的距离
的距离![]() , .................................11分
, .................................11分
所以![]() . .........................12分
. .........................12分
令![]() ,
,![]() ,
,
![]() ,
,
|
|
|
|
|
|
| + | 0 | - |
|
|
| 极大 |
|
由上表可得![]() 最大值为
最大值为![]() . ................................13分
. ................................13分
所以当![]() 时,
时,![]() 的面积取得最大值
的面积取得最大值![]() . ..................................14分
. ..................................14分