如图，点O为矩形ABCD的对称中心，AB=10 cm，BC=12 cm，点E,F,G分别从A,B,C三点同时出发，沿矩形的边按逆时针方向匀速运动，点E的运动速度为1 cm/s，点F的运动速度为3 cm/s，点G的运动速度为1.5 cm/s，当点F到达点C(即点F与点C重合)时，三个点随之停止运动.在运动过程中，△EBF关于直
线EF的对称图形是△EB′F.设点E,F,G运动的时间为t(单位：s).
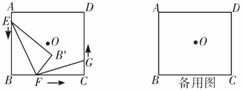
(1)当t=s时，四边形EBFB′为正方形；
(2)若以点E,B,F为顶点的三角形与以点F,C,G为顶点的三角形相似，求t的值；
(3)是否存在实数t，使得点B′与点O重合？若存在，求出t的值；若不存在，请说明理由.
解：(1)若四边形EBFB′为正方形，则BE=BF，即10-t=3t,解得t=2.5.
(2)分两种情况，讨论如下：
①若△EBF∽△FCG,
则有 
, 解得t=2.8；
②若△EBF∽△GCF,
则有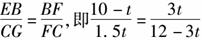 
,
解得t=-14-2 
(不合题意，舍去)或t=-14+2 
.
∴t=2.8s或t=(-14+2 ) s时，以点E,B,F为顶点的三角形与以点F,C,G为顶点的三角形相似.
(3)假设存在实数，使得点B′与点O重合
.
如图，过点O作OM⊥BC于点M，则在Rt△OFM中，OF=BF=3t,FM=BC-BF=6-3t,OM=5,由勾股定理得OM2+FM2=OF2,即52+(6-3t)2=(3t)2,解得t= 
.
如图，
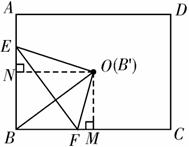
过点O作ON⊥AB于点N，则在Rt△OEN中，OE=BE=10-t,EN=BE-BN=10-t-5=5-t,ON=6,
由勾股定理得ON2+EN2=OE2,即62+(5-t)2=(10-t)2,解得t=3.9.
∵ 
≠3.9，∴不存在实数t,使得B′与点O重合.