(08年四川卷理)设等差数列
的前
项和为
，
，
，则
的最大值是 .
(08年四川卷理)设等差数列的前项和为，，，则的最大值是 .
答案：4．
解析：由题意，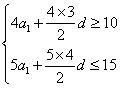
，即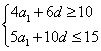
，
，
．
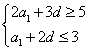这是加了包装的线性规划，有意思．建立平面直角坐标系
，画出可行域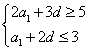（图略），画出目标函数即直线，由图知，当直线过可行域内
点时截距最大，此时目标函数取最大值
．本题明为数列，实为线性规划，着力考查了转化化归和数形结合思想．掌握线性规划问题＂画－移－求－答＂四步曲，理解线性规划解题程序的实质是根本．这是本题的命题意图．
因约束条件只有两个，本题也可走不等式路线．设
，由
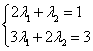解得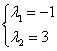
，∴
，由不等式的性质得：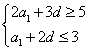 
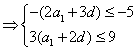
，即
，
的最大值是4．
从解题效率来看，不等式路线为佳，尽管命题者的意图为线性规划路线．本题解题策略的选择至关重要．
点评：
（1）二项式定理，直线和圆的方程，正四棱柱，数列几个知识点均为前两年未考点．
（2）无多选压轴题．无开放性压轴题．易入手，考不好考生只能怪自已．题出得基础，出得好，出得妙．尤其是第16题．